注意：最高性能的高精度在最后面的版本里。

介绍也有。

这里简单的介绍一下用法。

small_int<10000> a;

这表示我们声明了一个可以存储 $10^{10000}-1$ 的一个数组。

所以我们的用法应该是：

small_int<size> a;

那么，这里可存数字的范围就是 $-10^{size}+1 \to 10^{size}-1$ 的范围。

注意：只有可存数字范围相同的才可以互相进行运算，如果真的要，请先赋值再进行操作。

版本介绍

目前最高版本为：$1.3.01.04$ 版本或 $1.2.01.04$ 版本

注意：我们常用的高精度版本为 1.2.01.04 版本，只有碰到了特殊高精度才需要考虑 1.3.01.04 版本

而且在不是高精度乘低精度这种需要优化的方面上的话，是不需要换版本的。

$1.1.00.02$ 版本

特性：加法处理 $\mathcal O(n)$，减法处理 $\mathcal O(n)$，乘法处理 $\mathcal O(n^2)$，高精度除高精度处理 $\mathcal O(n^3)$，高精度除低精度处理 $\mathcal O(n)$，高精度乘低精度处理 $\mathcal O(n^2)$，高精 $mod$ 高精处理 $\mathcal O(n^3)$，拥有各种比较操作（除了不等于和非和与这种位运算），时间复杂度均为 $\mathcal O(n)$，且没有什么特别优化。

此版本介绍：

$pub\_max$ 函数：可以求最大值、最小值的函数。

但不过你需要先定义一个 $small\_int$，如：

我现在定义一个 $a$，访问方式即为 $a.pub\_max()$，有两个参数，都为 $small\_int$ 类型。

注意：这个函数只是返回他的最大值，并不会把这两个数的最大值赋值为自己。

$pub\_min$ 函数：和 $max$ 一样，只不过使用来求最小值的。

$pub\_int$ 函数：用来把 $long~long$ 类型（或者 $int$，整数类型除了 $unsigned~long~long$、$\_\_int128$ 都可以）给转化成 $small\_int$ 类型。

注意：这个函数也只是返回他转化后的样子，不会把这个数赋值给自己。访问方式如 $pub\_max$ 函数。

$in$ 函数：输入函数，没有参数。

$out$ 函数：输出函数，里面有一个参数，参数类型为 $string$，如果没有，默认输出换行，否则在输出完这个数字后会输出该参数里面的东西。

$size$ 函数：返回目前有几位的函数。（ $0$ 会被当成是 $1$ 位数）

$to\_empty$ 函数：清空本 $small\_int$ 里面的数字，即相当于把它变成 $0$。

注意：这个结构体里面的数字不会出现 $-0$，就算是你的输入是 $-0$，也不予理睬，只会是正 $0$。

$duru$ 函数：有 $string$ 参数类型，可以不需要输入，直接从字符串类型转换到 $small\_int$ 类型。

$+,-,\times,\div$ 函数：我们定义了 $small\_int$ 和 $small\_int$ 直接的相乘，也定义了 $small\_int$ 和 $long~long$ 直接的相乘。

注意事项 $1$：如果你要把 $small\_int$ 类型和 $long~long$ 类型直接相乘，请你先写 $small\_int$ 的类型变量，再写 $long~long$ 类型的变量，这样可以防止一些奇怪的编译错误。

注意事项 $2$：我们并没有定义 $+=,-=,\times=,\div=$ 这些符号以及 $<<,>>$ 这些位运算符号。

$\%$ 运算：取模，注意不能用负数取模。

我们定义了 $small\_int$ 和 $small\_int$ 直接的取模，也定义了 $small\_int$ 和 $long~long$ 直接的取模。

注意：$long~long$ 不可以取模 $small\_int$ 类型。

$==,>,<,<=,>=$ 等函数：比较运算符，也可以直接和 $long~long$ 比较。

注意事项 $1$：如果你要把 $small\_int$ 类型和 $long~long$ 类型直接比较，请你先写 $small\_int$ 的类型变量，再写 $long~long$ 类型的变量，这样可以防止一些奇怪的编译错误。

注意事项 $2$：我们并没有定义 $!=$ 符号。

$swap$ 函数：交换函数。

假设我现在定义一个 $small\_int$ 的变量 $a$ 和 $b$，现在我们想要交换 $a,b$，可以这样写：

$a.swap(b)$ 或 $b.swap(a)$。

但是请注意，假设我现在又有一个同样的类型 $c$，我们并不可以写 $c.swap(a),c.swap(b)$ 这一类的函数，这样会导致是 $c$ 和 $a$ 或 $b$ 交换，反而不是 $a$ 和 $b$ 交换。

代码。。

$1.3.01.04$ 版本

改进：可以求一个数的 $size$（长度），高精度乘低精度乘法优化到 $\mathcal O(n \times len)$，于 $2024$ 年 $4$ 月 $2$ 日优化到 $\mathcal O(n)$，$len$ 为低精度的那个数的长度；高精度除以高精度的除法优化到 $\mathcal O(n^2 \times \log10)$，高精 $mod$ 高精处理 $\mathcal O(n^2 \times \log 10)$，时间复杂度降了好多，可以使用其操作一些复杂的高精度功能，比较的时间复杂度也因此而降低。

此版本介绍：

$pub\_max$ 函数：可以求最大值、最小值的函数。

但不过你需要先定义一个 $small\_int$，如：

我现在定义一个 $a$，访问方式即为 $a.pub\_max()$，有两个参数，都为 $small\_int$ 类型。

注意：这个函数只是返回他的最大值，并不会把这两个数的最大值赋值为自己。

$pub\_min$ 函数：和 $max$ 一样，只不过使用来求最小值的。

$pub\_int$ 函数：用来把 $long~long$ 类型（或者 $int$，整数类型除了 $unsigned~long~long$、$\_\_int128$ 都可以）给转化成 $small\_int$ 类型。

注意：这个函数也只是返回他转化后的样子，不会把这个数赋值给自己。访问方式如 $pub\_max$ 函数。

$in$ 函数：输入函数，没有参数。

$out$ 函数：输出函数，里面有一个参数，参数类型为 $string$，如果没有，默认输出换行，否则在输出完这个数字后会输出该参数里面的东西。

$size$ 函数：返回目前有几位的函数。（ $0$ 会被当成是 $1$ 位数）

与上个版本不同的是，这个函数可以 $\mathcal O(1)$ 求出结果，但是上面的版本需要 $\mathcal O(n)$ 才能求出来。

$to\_empty$ 函数：清空本 $small\_int$ 里面的数字，即相当于把它变成 $0$。

注意：这个结构体里面的数字不会出现 $-0$，就算是你的输入是 $-0$，也不予理睬，只会是正 $0$。

$duru$ 函数：有 $string$ 参数类型，可以不需要输入，直接从字符串类型转换到 $small\_int$ 类型。

$+,-,\times,\div$ 函数：我们定义了 $small\_int$ 和 $small\_int$ 直接的相乘，也定义了 $small\_int$ 和 $long~long$ 直接的相乘。

与上个版本不同的是：$small\_int$ 和 $small\_int$ 直接运算的时候，除法从 $\mathcal O(n^3)$ 优化成了 $\mathcal O(\log 10 \times n^2)$，乘法的时间复杂度、加法的时间复杂度都有巨大的变化，模运算也如此。

注意事项 $1$：如果你要把 $small\_int$ 类型和 $long~long$ 类型直接相乘，请你先写 $small\_int$ 的类型变量，再写 $long~long$ 类型的变量，这样可以防止一些奇怪的编译错误。

注意事项 $2$：我们并没有定义 $+=,-=,\times=,\div=$ 这些符号以及 $<<,>>$ 这些位运算符号。

$==,>,<,<=,>=$ 等函数：比较运算符，也可以直接和 $long~long$ 比较。

注意事项 $1$：如果你要把 $small\_int$ 类型和 $long~long$ 类型直接比较，请你先写 $small\_int$ 的类型变量，再写 $long~long$ 类型的变量，这样可以防止一些奇怪的编译错误。

注意事项 $2$：我们并没有定义 $!=$ 符号。

$\%$ 运算：取模，注意不能用负数取模。

我们定义了 $small\_int$ 和 $small\_int$ 直接的取模，也定义了 $small\_int$ 和 $long~long$ 直接的取模。

注意：$long~long$ 不可以取模 $small\_int$ 类型。

$swap$ 函数：交换函数。

假设我现在定义一个 $small\_int$ 的变量 $a$ 和 $b$，现在我们想要交换 $a,b$，可以这样写：

$a.swap(b)$ 或 $b.swap(a)$。

但是请注意，假设我现在又有一个同样的类型 $c$，我们并不可以写 $c.swap(a),c.swap(b)$ 这一类的函数，这样会导致是 $c$ 和 $a$ 或 $b$ 交换，反而不是 $a$ 和 $b$ 交换。

上一个版本的 $bug$：

假设你开了个长度为 $20000$ 的 $small\_int$，但是里面的数只不过是 $long~long$ 范围的，这个 $bug$ 会导致这个东西乘起来会耗费 $O(n^2)$ 的时间，并且导致时间超过了一秒。但是，这个版本已经修复了这个 $bug$，并且时间复杂度更低了。

如果你试了，那你肯定知道：开了 $20000$ 确实会超时很严重。

但不过用上这个版本就不一样了。

输出部分的快慢已经通过调整。

之前的输出 $bug$：

假设我们定义一个变量 $a$，里面的数字是 $114514$，但不过因为你申请了一个 $2 \times 10^6$ 的空间，所以他会每次从 $2 \times 10^6-1$ 的地方开始循环。

然后，每次应该要循环到 $5$ 才停止，开始输出。

注意：他是倒序循环，每次 $--i$。

但是，假设你要输出 $1000$ 遍这个数，哪怕你开了 $O2$，恐怕也要超时。

现在，不会有这个问题了，因为我们维护了 $size$，直接从 $size-1$ 倒序输出即可。

这样就不会超时啦~

之前空间的 $bug$：

如果你在 $main$ 函数外面申请了一片空间，长度为 $3 \times 10^5$，他会立马爆掉。

为什么呢？

因为他用的是栈空间。

每一个变量都是用的占空间，这就导致了空间非常受限。

所以，我特地修复了这个 $bug$，用 $vector$ 存了起来。

代码。

$1.2.01.04$ 版本

这个地方不在赘述，和 $1.3.01.04$ 版本几乎没有任何差别。（除了高精度时间复杂度）

这也是非常常用的高精度模版。但是 $1.3.01.04$ 为不常用模版。

只不过是高精度乘低精度的时间复杂度为 $\mathcal O(n \times len)$ 而已，并未多大影响。

代码。

$Update：$

$2024$ 年 $4$ 月 $2$ 日：经过检查，每个版本均可正常运行，可以投入到正常的使用中了，于今日彻底完成这两个版本，更新了每一个版本的高精度功能介绍。

我们还更新了输出、空间方面的 $bug$。

$2024$ 年 $4$ 月 $2$ 日 $18$ 点 $13$ 分：因为我在拿这个高精度做某道题（自行查看）的时候，成功超时，最后只能调整高精度乘低精度的策略，将时间复杂度从 $\mathcal O(n \times len)$ 优化到了 $\mathcal O(n)$。特殊版本 $1.3.01.04$ 也从此诞生。

在这里插播一个小事情：

假设你用 $1.2.01.04$ 版本去做洛谷 $P1932$，那么你会得到这个时间复杂度：

但不过你用特殊版本 $1.3.01.04$ 版本去做的话，结果是：

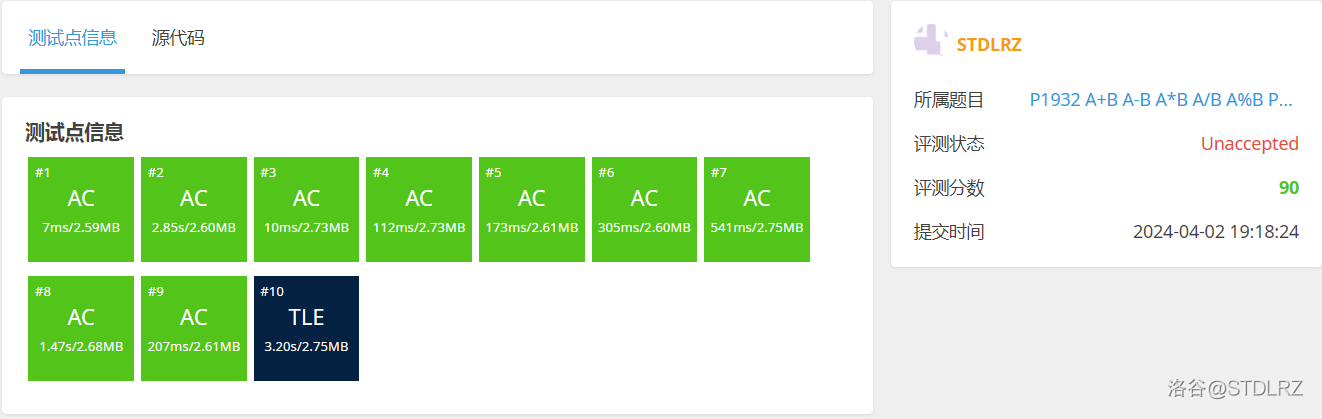
所以，只有在特殊情况下，再动用特殊版本。不然你可能会死的很惨

注：把 $1.3.01.04$ 版本中的 vector<long long> 改成 vector<int> 即可 $AC$，但不过还是有点慢。

$2024$ 年 $4$ 月 $3$ 日：

在这里插播一件小事情。

就是，有一些特殊的题目必须手写高精度，不可以套用模版。

如：这道题，你套用模版会取得：

但不过，你手写会：

虽然套模板可能确实很快乐，因为不用打高精度了，但不过贪心总有下场的。

所以，可以套模板，但是注意适度哦~