整理半小时,至森林处完结,可能有不全的瑕疵。

概念

• 图$G=(V,E)$为节点集$V$和边集$E$组成的二元组，描述$V$中节点间的相互关系。
• 节点($vertex$):一般图的节点数为n,则节点一般用整数$1,2,...,n$标记。
• 边($edge$):用无序数对$(u,v)$,或者表示成$u-v$,表示$u$与$v$间有边$(1≤u,v≤n)$。
• $e=(u,v)$可称$u$和$v$邻接,或可称$e$和$u$,$v$关联。

没有自环和重边的图称为简单图，在该图中任意边的两端都不是同一个节点，任意一对节点间最多被一条边连接。

• 节点的度数：与节点关联的边数。 每个节点的度不可能超过$n-1$,因此边数E的上限为

$$\frac{(n-1)×n}{2}$$

• 如果$E$达到上限，该图为完全图。

路径

• 图的一条路径指的是一个节点序列，该序列中的相邻节点在图上是邻接的。
• 如果节点和边都不重复出现，则称为简单路径；
• 若序列中除了起点和终点相同外没有重复节点和边，称为圈(亦称为环或回路)。
• 如果图中任意两点之间都有路径，则称该图是连通图；否则称该图是非连通图。非连通图有多个连通分量，每个连通分量是一个极大连通子图，因为任意增加一个节点以后将成为非连通图。
• 路径与路径之间有相交和不相交的关系。若路径间表示除了起点和终点外没有公共点，则称为不相交路。更严格的定义是，任意节点都不相同的路径叫严格不相交路径；任意边都不相同的路径叫严格边不相交路。

分类

• 按照广义的分类,任何图都可分为无向图和有向图、无权图和加权图、稀疏图和稠密图。
• 按照狭义分类,图又可具体分为完全图和补图、树和森林、图的生成树和生成森林、平面图、二分图、相交图和区间图等特殊形态。

无向图:

在图$G=(V,E)$中,如果对于任意的$a,b∈V$时,当$(a,b)∈E$时,必有$(b,a)∈E$(即关系对称),则称此图为无向图。在一无向图中用不带箭头的边连接两个有关联的节点。

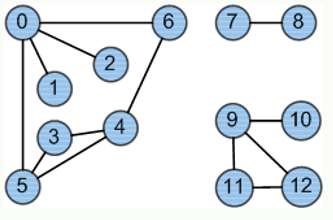
有向图:

有向图中的边都是单向的,因此边$(u,v)$是有序数对。有时用带箭头的弧专指有向边。在有向边$(u,v)$中,$u$和$v$分别叫源和目的。忽略有向图中所有边的方向,得到的无向图称为该有向图的基图。

无权图和加权图:

• 若图中的节点和边不带权,则称该图为无权图。
• 若给边或节点加权,则称该图为加权图或带权图。
• 可加多种权,通常代表费用、距离等,既可以是正数,也可以是负数。
• 加权有向图一般也称为网络。

完全图和补图:

• 若图的节点数为n,边数E达到$\frac{(n-1)×n}{2}$(即图中每个节点的度数为$n-1$),则称该图为完全图。
• 对于边($u$,$v$),若邻接则改为非邻接,若非邻接则改为邻接,得到的图为原图的补图。
• 原图和补图的并为完全图。完全子图称为团。

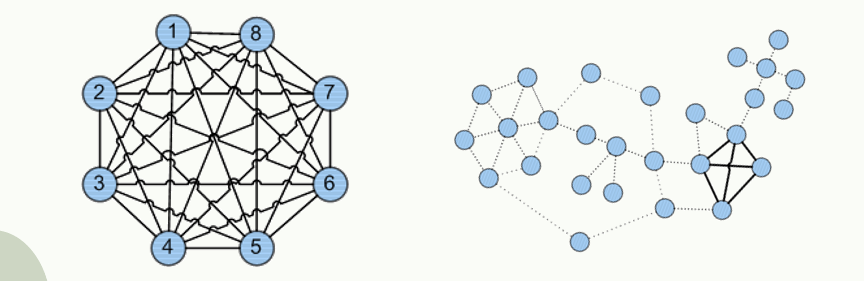
稀疏图和稠密图:

边数$E$远小于$\frac{(n-1)×n}{2}$的图称为稀疏图,它的补图为稠密图。稀疏图一般采用时间复杂度为$O(ElbE)$的算法;稠密图一般采用时间复杂度为$V2$的算法。

树和森林

不含圈的连通图称为树。树的集合称为森林。

树是图的一种特殊形态。一个图$G$是树当且仅当以下任意一个条件成立：

1. $G$有$v-1$条边,无圈
2. $G$有$v-1$条边,连通
3. 任意两点只有唯一的简单路径
4. $G$连通,但任意删除一条边后不连通

题目

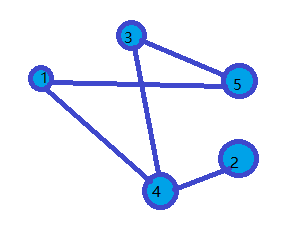
♥在一个无向图中,如果任意两点之间都存在路径相连,则称其为连通图。右图是一个有$5$个顶点、$8$条边的连通图。 若要使它不再是连通图,至少要删去其中的___条边。

$A.2$

$B.3$

$C.4$

$D.5$

答案:$B$。

删去度最小的边

---

♥$G$是一个非连通无向图(没有重边和自环),共有$28$条边,则该图至少有___个顶点。

$A.10$

$B.9$

$C.11$

$D.8$

答案:B

$\frac{8×(8-1)}{2}=28$,但是无向图,所以还有一个孤点,$8+1=9$。

---

♥在无向图中，所有顶点的度数之和是边数的( ) 倍。

$A.0.5$

$B.1$

$C.2$

$D.4$

答案:C

没啥好说的了...

---

♥由四个不同的点构成的简单无向连通图的个数是( )。

$A.32$

$B.35$

$C.38$

$D.41$

答案:C

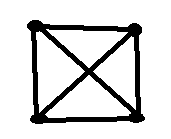
先构建一个无向联通图,看看可以删几条边。

• 删$0$条:$1$种
• 删$1$条:$6$种
• 删$2$条:$C^2_6=15$(种)
• 删$3$条:$C^3_6$-4$=20$(种),要减去删完导致为非连通图的情况
• 删$4$条:$0$种
• ...

$∴$有$1+6+15+20=38$(种)。

---

♥设$G$是有$n$个结点、$m$条边($n≤m$)的连通图,必须删去$G$的( ) 条边,才能使得G变成一棵树。

A.$m-n+1$

B. $m-n$

C. $m+n+1$

D. $n-m+1$

代码模板:

遍历

广搜:

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

int n,m,u,v;
bool vis[101];//判重

vector <int> g[101];//存节点
queue <int> q;

void bfs(int u)
{
	q.push(u);//广搜标准代码
	vis[u] = true;
	while(!q.empty())
	{
		int f = q.front();//取头
		cout << f << ' ';
		q.pop();
		for(int i = 0;i < g[f].size();i++)
		{
			int v = g[f][i];
			if(!vis[v])
			{
				vis[v] = true;//设为已过
				q.push(v);
			}
		}
	}
}

signed main()
{
	cin >> n >> m;
	for(int i = 1;i <= m;i++)
	{
		cin >> u >> v;
		g[u].push_back(v);
		g[v].push_back(u);
	}
	for(int i = 1;i <= n;i++)
	{
		if(!vis[i]) bfs(i);//广搜
	}
	return 0;
}

深搜:

#include <iostream>
#include <vector>
using namespace std;

int n,m,u,v,a[101][101];
bool vis[101];

void dfs(int u)
{
	cout << u << ' ';//输出
	vis[u] = true;
	for(int i = 1;i <= n;i++) if(a[u][i] == 1 && !vis[i]) dfs(i);//爱死了
	return;
}

signed main()
{
	cin >> n >> m;
	for(int i = 1;i <= m;i++)
	{
		cin >> u >> v;
		a[u][v]++;
		a[v][u]++;
	}
	for(int i = 1;i <= n;i++)
	{
		if(!vis[i]) dfs(i);
	}
	return 0;//没啥好说的了
}

链式

#include <iostream>
#include <cstring>
using namespace std;

int n,m,tot,u,v,head[101];
bool vis[101];

struct node
{
	int u;
	int v;
	int next;
	
}edge[1001];

void addg(int u,int v)
{
	edge[++tot].u = u;
	edge[tot].v = v;
	edge[tot].next = head[u];
	head[u] = tot;
}

void dfs(int u)
{
	vis[u] = true;
	cout << u << ' ';
	for(int i = head[u];i != -1;i = edge[i].next)
	{
		int v = edge[i].v;
		if(!vis[i]) dfs(v);
	}
}

int main()
{
	cin >> n >> m;
	memset(head,-1,sizeof(head));
	for(int i = 1;i <= m;i++)
	{
		cin >> u >> v;
		addg(u,v);
		addg(v,u);
	}
	dfs(1);
	return 0;
}

mini拓展:

∵二叉树是一种特殊的树,又∵树是一种特殊的图,∴二叉树是一种特殊的特殊的图/doge。

二叉树：

概念: 每个根都有至多$2$个子结点的树。

满二叉树:每个根都有$2$个或$0$个子结点的二叉树。(结点数:$2^{n-1}$)

完全二叉树:任意按照广搜顺序生长排列的二叉树。即除树的最底层外的层的每一个根都有$2$个子结点

只有一个节点,是完全也是满二叉树。

遍历:

• 前序遍历:根→左→右
• 中序遍历:左→根→右
• 后序遍历:左→右→根

确实很简略,有不好处请评论(该死根本不能评论

人生是张稠密的连通图，

没有一个节点叫做失败。

哪怕找不到最短路，

前方依然是通途