一个很优美的东西。主要用于在动态数组中求区间和。

关于 lowbit()

$\texttt{lowbit}(x)$ 指的是 $x$ 的二进制表达式中最右边 $1$ 所对应的值。即 $x$ 与上 $(-x)$ 的值。

证明：

可以发现，$x$ 为奇数时，$\texttt{lowbit}(x)=1$，否则，$\texttt{lowbit}(x)=$ 最后一个 $1$ 后面一堆 $0$。因为偶数二进制补码最后一位一定是 $1$，就会有进位。

树

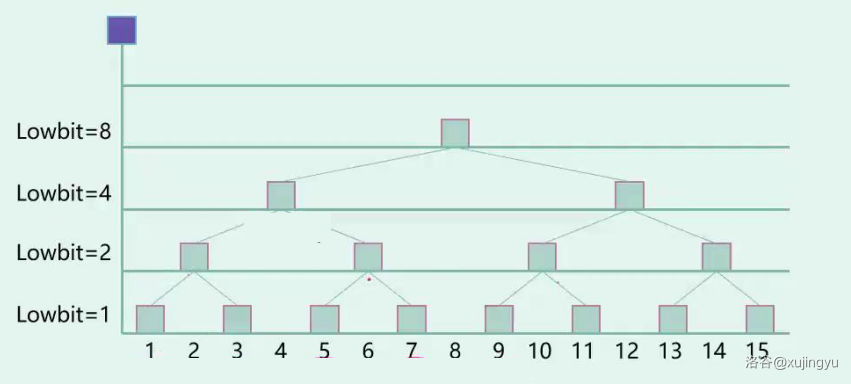
根据 lowbit() 建树。若要查询一个节点 $x$ 的关系节点：

• 父节点：

  • 若 $x$ 为左儿子，就将 $x+\texttt{lowbit}(x)$；
  • 若为右儿子，则 $x-\texttt{lowbit}(x)$。

• 儿子节点：

  • 左儿子：$x-\dfrac{x}{2}$；
  • 右儿子：$x+\dfrac{x}{2}$。

代码

若要修改某个值，则需要将其关联的区间全部修改。

需要从下往上爬，不断找右上方的节点（不一定按照边找父亲）。途径的每个节点都需要加上给出的值。最终一直加到 $n$ 以后才结束。

void modify(int x,int d)//修改
{
	while(x <= n)
	{
		c[x] += d;
		x += lowbit(x);
	}
	return;
}

若要查询和，则不停找左上角的值。但要保证现在的节点编号大于 $0$。

int sum(int x)//求和
{
	int dig = 0;
	while(x >= 1)
	{
		dig += c[x];
		x -= lowbit(x);
	}
	return dig;
}

综合：

int lowbit(int x)//函数
{
	return x & (-x);
}
void modify(int x,int d)
{
	while(x <= maxn)
	{
		c[x] += d;
		x += lowbit(x);
	}
	return;
}
int sum(int x)
{
	int dig = 0;
	while(x >= 1)
	{
		dig += c[x];
		x -= lowbit(x);
	}
	return dig;
}