基础

问题类型

动态区间修改查询类问题。如：给定一个 $n$ 个元素的数组 $a_1,a_2,\dots,a_n$，现有两种操作：

1. update 操作：把 $a_x$ 修改为 $y$；
2. query 操作：给出 $l$ 和 $r$，计算 $\min\limits^r_{i=l}a_i$。

结构

定义：

• 区间：用一对数 $a$、$b$ 表示一个区间 $[a,b]$（或 $(a,b]$）。
• 节点 $T(a,b)$：表示该节点维护了区间 $[a,b](a\leq b$ 且均为整数 $)$ 的信息。
• 内部节点：$T(a,b)$ 的左儿子为 $T(a,\dfrac{a+b}{2})$；右儿子为 $T(\dfrac{a+b}{2}+1,b)$
• 叶节点：若 $T(a,b)$ 中 $a=b$，则 $T(a,b)$ 为叶节点。

线段树结构以递归维护。

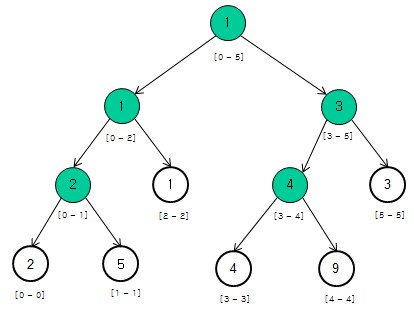
（图片来源于 https://www.cnblogs.com/TenosDoIt/p/3453089.html）

建树：

void build(int o,int l,int r)
{
	if(l == r)//叶子节点
	{
		s[o] = a[l];
		return;
	}
	int mid = (l + r) / 2;//中间
	build(o * 2,l,mid);//左儿子
	build(o * 2 + 1,mid + 1,r);//右儿子
	work(o);//处理
	return;
}

注意：存线段树结构的数组或链表至少要开到线段长度的四倍大。

性质

性质：

• 若线段树处理的数列长度为 $n$（即根节点区间为 $[1,n]$），那么总结点不超过 $2n$ 个。
• 深度：看做满二叉树，不超过 $log(2\times n)$
• 线段分解数量级：查询大多都能在 $\mathcal{O(logn)}$ 时间内解决。

查询代码：

int query(int o,int l,int r,int x,int y)//也可以是bool,long long等类型
{
	if(l >= x && r <= y) return s[o];//目标区间完全覆盖当前区间
	int mid = (l + r) / 2;//中间
	if(x <= mid) /*递归处理*/;
	if(y > mid) /*递归处理*/;
	return /*根据情况决定*/;
}

储存

储存：

1. 链表储存
2. 数组模拟链表
3. 堆结构储存

修改代码：

修改需要将包含该位置的所有区间修改。

void update(int o,int l,int r,int x,int y)
{
	if(l == r)//叶结点
	{
		s[o] = y;//修改
		return;
	}
	int mid = (l + r) / 2;//中间
	if(x <= mid) update(o * 2,l,mid,x,y);//在左儿子区间
	else update(o * 2 + 1,mid + 1,r,x,y);
	work(o);
	return;
}

代码

void work(int rt)//处理
{
	/**/;
	return;
}

void build(int o,int l,int r)//建树
{
	if(l == r)
	{
		s[o] = a[l];
		return;
	}
	int mid = (l + r) / 2;
	build(o * 2,l,mid);
	build(o * 2 + 1,mid + 1,r);
	work(o);
	return;
}
void update(int o,int l,int r,int x,int y)//修改
{
	if(l == r)
	{
		s[o] = y;
		return;
	}
	int mid = (l + r) / 2;
	if(x <= mid) update(o * 2,l,mid,x,y);
	else update(o * 2 + 1,mid + 1,r,x,y);
	work(o);
	return;
}
int query(int o,int l,int r,int x,int y)//查询
{
	if(l >= x && r <= y) return s[o];
	int mid = (l + r) / 2;
	/**/;
	return /**/;
}

权值线段树

对权值进行处理的线段树模型，节点统计值出现的次数。

const int maxN = 1e7;
int n,a[10000001],g[40000001],tree[40000001];

void update(int o,int l,int r,int x,int v)
{
	if(l == r)
	{
		tree[o] += v;
		return;
	}
	int mid = (l + r) / 2;
	if(x <= mid) update(o * 2,l,mid,x,v);
	else update(o * 2 + 1,mid + 1,r,x,v);
	tree[o] = tree[o * 2] + tree[o * 2 + 1];
	return;
}

int query(int o,int l,int r,int x,int y)//查询值域x,y间存在的个数
{
	if(y < l || r < x) return 0;
	if(x <= l && r <= y) return g[o];
	int mid = (l + r) / 2;
	int s1 = query(o * 2,l,mid,x,y);
	int s2 = query(o * 2 + 1,mid + 1,r,x,y);
	return s1 + s2;
}

int Count(int o,int l,int r,int x)//查询某一点个数
{
	if(l == r) return g[o];
	int mid = (l + r) / 2;
	if(x <= mid) return Count(o * 2,l,mid,x);
	else return Count(o * 2 + 1,mid + 1,r,x);
}

int kth(int o,int l,int r,int k)//查询第k大的数
{
	if(l == r) return r;
	int mid = (l + r) / 2;
	if(k <= g[o * 2]) return kth(o * 2,l,mid,k);
	else return kth(o * 2 + 1,mid + 1,r,k - g[o * 2]);
}

int pre_val(int x)//查询某数的前驱
{
	int k = query(1,1,maxN,1,x - 1);
	if(!k) return -1;
	return kth(1,1,maxN,k);
}

int nxt_val(int x,int i)//后继
{
	int k = query(1,1,maxN,1,x) + 1;
	if(k == i) return -1;//注意条件,不同操作不同判断
	return kth(1,1,maxN,k);
}