真理：如果你会图论，你就会树；如果你会数组、循环，你就会 dp；结合起来，树上 dp 对你来说就是小意思啦！

树的定义

树满足以下三个条件：

• $n$ 个节点 $n-1$ 条边；
• 连通图；
• 无环无重边无自环。

没有固定根节点的数称为无根树（$\textbf{unrooted\ tree}$）；

指定一个节点为根，则形成一棵有根树（$\textbf{rooted\ tree}$）。

树的其它定义：

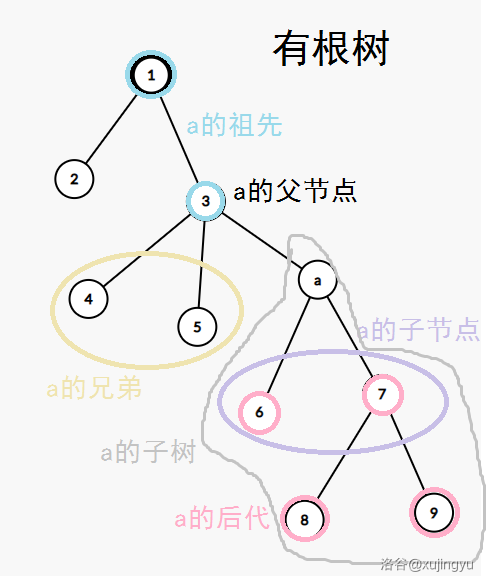
树的重心（质心）

定义

对于一棵 $n$ 个节点的无根树，找到一个点，使得把树变成以该节点为根的有根树时，最大子树的节点数最小。换句话说，删除这个点后最大连通块的节点数最小。

实现

1. 任选一个节点作为根，把无根树变成有根树；
2. 设 $siz_i$ 表示以 $i$ 为根的子树的节点个数，则 $siz_i=\sum\limits_{j\in son(i)}siz_j+1$；
3. 节点 $i$ 的子树中最大的有 $\max(d_j)$ 个节点，$i$ 的“上方子树”中有 $n-d_i$ 个节点。

模板题黑手党：

#include <bits/stdc++.h>
using namespace std;

int n,siz[50001],weight[50001],cen[2],minn = 1e9;
//该节点的大小,即子树的所有节点+该节点;
//该节点的重量,即所有子树大小最大值
//节点重心
vector <int> g[50001];

void dfs(int u,int fa)
{
	siz[u] = 1;
	weight[u] = 0;
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		if(v == fa) continue;
		dfs(v,u);
		siz[u] += siz[v];
		weight[u] = max(weight[u],siz[v]);
	}
	weight[u] = max(weight[u],n - siz[u]);//向上子树
	if(weight[u] < minn)
	{
		cen[0] = u;
		minn = weight[u];
	}
	else if(weight[u] == minn) cen[1] = u;
	return;
}

signed main()
{
	scanf("%d",&n);
	for(int i = 1;i < n;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		g[u].push_back(v);
		g[v].push_back(u);
	}
	dfs(1,-1);
	if(weight[cen[1]] != weight[cen[0]]) printf("%d",cen[0]);
	else printf("%d %d",min(cen[0],cen[1]),max(cen[0],cen[1]));
	return 0;
}

性质

1. 一个点是重心，等价于以这个点为根，它的每个子树的大小，都不会超过整个树大小的一半；
2. 树中所有点到某个点的距离和中，到重心的距离和是最小的；如果有两个重心，那么它们的距离和一样；
3. 把两个树通过一条边相连得到一个新的树，那么新的树的重心在连接原来两个树的重心的路径上；
4. 把一个数添加或删除一个叶子，那么它的重心最多只移动一条边的距离；
5. 树的重心如果不唯一，则至多有两个，且这两个重心相邻。

树的直径

定义

对于一棵 $n$ 个节点的无根树，找到一条最长路径。换句话说，要找到两个点，使得它们的距离最远。一棵树可以有多个直径。

证明：考虑这样一棵树，我们假设 $AB$ 是树的直径，$C$ 的最远点为 $D$，那么有 $AC<CD$，$a+c<d$，因为 $c>0$，所以 $a<d+c$，故有 $a+b<b+c+d$，$AB<BD$，与假设 $AB$ 是直径矛盾，故性质得证。

实现

一：

对于权值均为正的树，我们任取树中一个节点 $x$，找出距离它最远的点 $y$，那么 $y$ 就是这棵树中一条直径的一个端点。我们再从 $y$ 出发，找出距离 $y$ 最远的点就找到了一条直径。这个算法依赖于一个性质：对于树中任意一个点，距离它最远的点一定是树上一条直径的一个端点。

#include <bits/stdc++.h>
using namespace std;

void dfs(int u,int fa)
{
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		if(v == fa) continue;
		d[v] = d[u] + 1;
		if(d[v] > d[c]) c = v;
		dfs(v,u);
	}
	return;
}

signed main()
{
	//任取一点开始dfs,选取节点1
	dfs(1,-1);
	d[c] = 0;
	dfs(c,0);
	return 0;
}

二：树形 dp

1. 先把无根树转化为有根树。对于任意节点 $i$，经过 $i$ 的最长路径就是链接 $i$ 的两颗不同子树 $u$ 和 $v$ 的最深叶子的路径；
2. 设 $d_i$ 表示节点 $i$ 的子树中根到叶子的最大距离，则 $d_i=\max(d_j)+1$；
3. 对于每个节点 $i$，把所有子节点的 $d_j$ 都求出来之后，设 $d$ 值前两大的节点 $u$ 和 $v$，则 $d_u+d_v+2$ 就是所求。

树形 dp 可以在存在负权边的情况下求解出树的直径。

#include <bits/stdc++.h>
using namespace std;

void dfs(int u,int fa)
{
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		if(v == fa) continue;
		dfs(v,u);
		d = max(d,dp[u] + dp[v] + 1);
		dp[u] = max(dp[u],dp[v] + 1)
	}
	return;
}

signed main()
{
	dfs(1,-1);
	return 0;
}

模板题奶牛马拉松：

#include <bits/stdc++.h>
using namespace std;

int n,m,d = -1,dp[40001];
char c;
struct node
{
	int v,w;
};
vector <node> g[40001];

void dfs(int u,int fa)
{
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i].v;
		int w = g[u][i].w;
		if(v == fa) continue;
		dfs(v,u);
		d = max(d,dp[u] + dp[v] + w);
		dp[u] = max(dp[u],dp[v] + w);
	}
	return;
}

signed main()
{
	scanf("%d%d",&n,&m);
	for(int i = 1;i <= m;i++)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		cin >> c;
		g[u].push_back((node){v,w});
		g[v].push_back((node){u,w});
	}
	dfs(1,-1);
	printf("%d",d);
	return 0;
}

树的最大独立集

动态规划必须满足的条件：

1. 阶段性；
2. 最优子结构性质；
3. 无后效性。

树的最大独立集

独立集，即对于一课 $n$ 个节点的无根树，选出尽量多的节点，使得任何两个节点均不相邻。

解法

例题：拜访奶牛 or 没有上司的舞会。

设 $dp_{i,0/1}$ 代表以 $i$ 为根的子树的最优解。第二维值为 $1$ 代表选入 $i$，否则不选入 $i$。

对于每个状态：

• 若选 $i$，$i$ 相邻的都不可以选。$dp_{i,1}=\sum\limits_{j\in son(i)}dp_{j,0}+value_i$；
• 若不选，$i$ 相邻的可以选，也可以不选。$dp_{i,0}=\sum\limits_{j\in son(i)}\max(dp_{j,0},dp_{j,1})$。

#include <bits/stdc++.h>
using namespace std;

int n,d[50001],dp[50001][2];
vector <int> g[50001];

void dfs(int u)
{
	dp[u][0] = 0;//初始化
	dp[u][1] = 1;
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		dfs(v);
		dp[u][0] += max(dp[v][0],dp[v][1]);
		dp[u][1] += dp[v][0];
	}
	return;
}

signed main()
{
	scanf("%d",&n);
	for(int i = 1;i < n;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		g[v].push_back(u);
		d[u]++;
	}
	int root = 1;
	for(int i = 1;i <= n;i++)
	{
		if(!d[i])
		{
			root = i;
			break;
		}
	}
	dfs(root);
	printf("%d",max(dp[root][0],dp[root][1]));
	return 0;
}

树的最小点覆盖

给定一棵树，给定一个点集 $V$，要求每条边至少有一个顶点在点集 $V$ 中，求最小的点集 $V$。

设

• $dp_{u,0}$ 表示以 $u$ 为根的子树且 $u$ 属于点覆盖集合的最小数量；
• $dp_{u,1}$ 表示以 $u$ 为根的子树且 $u$ 不属于点覆盖集合的最小数量；
• $v$ 为 $u$ 儿子。

则

• $dp_{u,0}=\sum\min(dp_{v,0},dp_{v,1})+1$；
• $dp_{u,1}=\sum dp_{v,0}$。

树的最小支配集

对于图 $G=(V,E)$ 来说，最小支配集指的是从 $V$ 中取尽量少的点组成一个集合，使得对于 $V$ 中剩余的点都与取出来的点有边相连。

根据定义可得出：最小点覆盖一定是最小支配集，但最小支配集不一定是最小点覆盖；最小点覆盖是点覆盖边，最小支配集是点支配点。

设：

• $dp_{u,0}$ 为 $u$ 在支配集中的最优方案；
• $dp_{u,1}$ 为 $u$ 不在支配集中，但子节点在支配集中的最优方案；
• $dp_{u,2}$ 为 $u$ 不在支配集中，但父节点在支配集中的最优方案；

得出：

• $dp_{u,0}=\sum\min(dp_{v,0},dp_{v,1},dp_{v,2})$；
• $dp_{u,1}=\sum\min(dp_{v,0}+dp_{v,2})$；
• $dp_{u,2}=\sum\min(dp_{v,0}+dp_{v,1})$。

例题：战略游戏 or 战略游戏：

#include <bits/stdc++.h>
using namespace std;

int n,dp[1501][3];
vector <int> g[1501];

void dfs(int u,int fa)
{
	dp[u][0] = 1;
	dp[u][1] = 0;
	dp[u][2] = 1e9;
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		if(v == fa) continue;
		dfs(v,u);
		dp[u][0] += min(dp[v][0],min(dp[v][1],dp[v][2]));
		dp[u][1] += min(dp[v][0],dp[v][2]);
		dp[u][2] += min(dp[v][0],dp[v][1]);
	}
	return;
}

signed main()
{
	scanf("%d",&n);
	for(int i = 1;i <= n;i++)
	{
		int u,k,v;
		scanf("%d%d",&u,&k);
		for(int j = 1;j <= k;j++)
		{
			scanf("%d",&v);
			g[u].push_back(v);
			g[v].push_back(u);
		}
	}
	dfs(1,-1);
	printf("%d",min(dp[1][0],min(dp[1][1],dp[1][2])));
	return 0;
}

例题：小胖守皇宫 or 保安站岗：

#include <bits/stdc++.h>
using namespace std;

int n,dp[1501][3],k[1501];
vector <int> g[1501];

void dfs(int u,int fa)
{
	dp[u][0] = k[u];
	dp[u][1] = 0;
	dp[u][2] = 1e9;
	int minn = 1e9,sum = 0;
	bool flag = false;
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		if(v == fa) continue;
		dfs(v,u);
		dp[u][0] += min(dp[v][0],min(dp[v][1],dp[v][2]));
		sum += min(dp[v][0],dp[v][2]);
		dp[u][2] = sum;
		if(dp[v][0] <= dp[v][2]) flag = true;
		if(dp[v][2] < dp[v][0]) minn = min(minn,dp[v][0] - dp[v][2]);
	}
	if(!flag && minn != 1e9) dp[u][2] += minn;
	dp[u][1] = sum;
	return;
}

signed main()
{
	scanf("%d",&n);
	for(int i = 1;i <= n;i++)
	{
		int u,aaa,m,v;
		scanf("%d%d%d",&u,&aaa,&m);
		k[u] = aaa;
		while(m--)
		{
			scanf("%d",&v);
			g[u].push_back(v);
			g[v].push_back(u);
		}
	}
	dfs(1,-1);
	printf("%d",min(dp[1][0],dp[1][2]));
	return 0;
}

换根 dp

又叫二次扫描，是树形 dp 的一种。

往往需要以不同的点为根求解问题，且节点的部分属性会受根的变化影响，如子节点深度和、点权和等。

因此无法通过一次搜索完成答案的求解，因为一次搜索只能得到一个节点的答案。

例题：根。

首先以节点 $1$ 为根，先做一次 dfs，求出所有节点的深度 $dep_u$ 以及每个节点对应子树的大小 $siz_u$，其中 $dep_u=\max\limits_{v\in son(u)}(dep_v)+1$，$siz_u=1+\sum\limits_{v\in son(u)}siz_v$。

令 $dp_u$ 为以 $u$ 为根时候的答案，即所有节点的深度和。现在可以得到 $dp_1$。

考虑“换根”，从父节点转移到子节点，$dp_u$ 转移到 $dp_v$。显然在换根的转移过程中，以 $v$ 为根或者以 $u$ 为根会导致其子树中的节点的深度产生改变，具体表现为：

• 所有在 $v$ 子树上的节点深度都减少了 $1$，那么总深度和就减少了 $siz_v$。
• 所有不在 $v$ 子树上的节点深度都增加了 $1$，那么总深度和就增加了 $n-siz_v$。

所以有：$dp_v=dp_u-siz_v+n-siz_v=dp_u+n-2\times siz_v$。

#include <bits/stdc++.h>
using namespace std;

int n,siz[1000001],dep[1000001],dp[1000001];
vector <int> g[1000001];

void tion(int u,int fa)
{
	siz[u] = 1;
	dep[u] = dep[fa] + 1;
	dp[1] += dep[u];
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		if(v == fa) continue;
		tion(v,u);
		siz[u] += siz[v];
	}
	return;
}
void dfs(int u,int fa)
{
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		if(v == fa) continue;
		dp[v] = dp[u] - siz[v] * 2 + n;
		dfs(v,u);
	}
	return;
}

signed main()
{
	scanf("%d",&n);
	for(int i = 1;i < n;i++)
	{
		int u,v;
		scanf("%d%d",&u,&v);
		g[u].push_back(v);
		g[v].push_back(u);
	}
	tion(1,0);
	dfs(1,0);
	int maxn = -1,sit = 1;
	for(int i = 1;i <= n;i++)
	{
		if(dp[i] > maxn)
		{
			maxn = dp[i];
			sit = i;
		}
	}
	printf("%d",sit);
	return 0;
}

树上背包

树上背包，顾名思义，就是在树上做背包问题。

例题：选课 or 选课。

设 $dp_{u,i,j}$ 表示以节点 $u$ 为根的子树的物品，考虑了 $u$ 的前 $i$ 个子节点在容量不超过 $j$ 时可以获得的最大价值。

由于只有选择了根节点，才会继续往下遍历，所以在遍历到 $u$ 节点时，先考虑一定选上它。$dp_{u,i,j}=\max(dp_{u,i,j},dp_{u,i-1,j-k}+dp_{v,i-1,k})$。

#include <bits/stdc++.h>
using namespace std;

int n,m,dp[301][301];
vector <int> g[301];

void dfs(int u)
{
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		dfs(v);
	}
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		for(int j = m;j >= 1;j--)
		{
			for(int k = 0;k < j;k++) dp[u][j] = max(dp[u][j],dp[u][j - k] + dp[v][k]);
		}
	}
	return;
}

signed main()
{
	scanf("%d%d",&n,&m);
	m++;
	for(int i = 1;i <= n;i++)
	{
		int u;
		scanf("%d%d",&u,&dp[i][1]);
		g[u].push_back(i);
	}
	dfs(0);
	printf("%d",dp[0][m]);
	return 0;
}

例题：有线电视网 or 有线电视网。