亮色主题 暗色主题

纯手打（悲）

同余

定义

设整数 $m\ne0$。若 $m\mid(a,b)$，称 $m$ 为模数（模），$a$ 同余于 $b$ 模 $m$，$b$ 是 $a$ 模 $m$ 的剩余，记作 $a\equiv b\mod m$，这样的等式，称为模 $m$ 的同余式，简称同余式。

性质

• 自反性：$a\equiv a\mod m$。
• 对称性：若 $a\equiv b\mod m$，则 $b\equiv a\mod m$。
• 传递性：若 $a\equiv b\mod m$，$b\equiv c\mod m$，则 $a\equiv c\mod m$。
• 线性运算：若 $a,b,c,d\in \mathbf{Z}$，$m\in \mathbf{N}^*$，$a\equiv b(\mod m)$，$c\equiv d(\mod m)$ 则有：
  • $a\mp c\equiv b\mp d(\mod m)$。
  • $a\times c\equiv b\times d(\mod m)$。
• 若 $a,b\in \mathbf{Z}$，$k,m\in \mathbf{N}^*$，$a\equiv b(\mod m)$，则 $ak\equiv bk(\mod mk)$。
• 若 $a,b\in \mathbf{Z}$，$d,m\in \mathbf{N}^*$，$d\mid a$，$d\mid b$，$d\mid m$，则当 $a\equiv b\mod m$ 成立时，有 $\dfrac{a}{d}\equiv \dfrac{b}{d}\mod \dfrac{m}{d}$。
• 若 $a,b\in \mathbf{Z}$，$d,m\in \mathbf{N}^*$，$d\mid m$，则当 $a\equiv b\mod m$ 成立时，有 $a\equiv b\mod d$。
• 若 $a,b\in \mathbf{Z}$，$d,m\in \mathbf{N}^*$，则当$a\equiv b\mod m$ 成立时，有 $\gcd(a,m)=\gcd(b,m)$。若 $d$ 能整除 $m$ 及 $a$，$b$ 中的一个，则 $d$ 必定能整除 $a$，$b$ 中的另一个。

如果一个线性同余方程 $ax\equiv1(\mod b)$，则 $x$ 称为 $a\mod b$ 的逆元，记作 $a^{-1}$。

数论函数

数论函数指定义域为正整数的函数。数论函数也可以视作一个数列。

积性函数

定义

若函数 $f(n)$ 满足 $f(1)=1$ 且 $∀x,y\in\mathbf{N}^*$，$\gcd(x,y)=1$ 都有 $f(xy)=f(x)f(y)$，则 $f(n)$ 为积性函数。

若函数 $f(n)$ 满足 $f(1)=1$ 且 $∀x,y\in\mathbf{N}^*$ 都有 $f(xy)=f(x)f(y)$，则 $f(n)$ 为完全积性函数。

性质

解释

若 $f(x)$ 和 $g(x)$ 均为积性函数，则以下函数也为积性函数：

$$h(x)=f(x^p)$$ $$h(x)=f^p(x)$$ $$h(x)=f(x)g(x)$$ $$h(x)=\sum\limits_{d\mid x}f(d)g(\dfrac{x}{d})$$

设 $x=∏p_i^{k_i}$

若 $F(x)$ 为积性函数，则有 $F(x)=∏F(p_i^{k_i})$。

若 $F(x)$ 为完全积性函数，则有 $F(x)=∏F(p_i)^{k_i}$。

例子

• 单位函数：$\varepsilon(n)=[n=1]$。（完全积性）
• 恒等函数：$id_k(n)=n^k$，$id_1(n)$ 同常记作 $id(n)$。（完全积性）
• 常数函数：$1(n)=1$。（完全积性）
• 除数函数：$\sigma_k(n)=\sum\limits_{d\mid n}d^k$。$\sigma_0(n)$ 通常记作 $d(n)$ 或 $\tau(n)$。$\sigma_1(n)$ 通常记作 $\sigma(n)$。

欧拉函数

定义

• 欧拉函数（Euler's totient function），即 $φ(n)$，表示的是小于等于 $n$ 和 $n$ 互质的数的个数。
• 形式化的表示：$φ(n)=\sum\limits_{i=1}^n[\gcd(i,n)=1]$
• $φ(n)=1$。

n	1	2	3	4	5	6	7	8	9	10
$φ(n)$	1		2		4	2	6	4	6	4

递推式：$φ(n)=n\times∏(1-\dfrac{1}{p_i})$

性质

欧拉函数是积性函数。

若 $n=p^k$，其中 $p$ 是质数，那么 $φ(n)=p^k-p^{k-1}$。（根据定义可知）

由唯一分解定理，设 $n=∏\limits_{i-1}^sp_i^{k_i}$，其中 $p_i$ 是质数，有 $φ(n)=n\times∏\limits_{i-1}^s\dfrac{p_i-1}{p_i}$。

计算单个数的欧拉函数值

int euler_phi(int n)
{
	int ans = n;
	for(int i = 2;i * i <= n;i++)
	{
		if(n % i == 0)
		{
			ans = ans / i * (i - 1);
			while(n % i == 0) n /= i;
		}
	}
	if(n > 1) ans = ans / n * (n - 1);
	return ans;
}

筛法求欧拉函数

• 每一个合数 $n$ 都是被最小的质因子 $p_j$ 筛掉
• 考虑 $n/p_j$ 是否能整除 $p_j$

void pre(int n)
{
	phi[1] = 1;
	int cnt = 0;
	for(int i = 2;i <= n;i++)
	{
		if(!not_prime[i])
		{
			prime[cnt++];
			phi[i] = i - 1;
		}
		for(int j = 0;j < cnt;j++)
		{
			if(i * prime[j] > n) break;
			not_prime[i * prime[j]] = true;
			if(i % prime[j] == 0)
			{
				phi[i * prime[j]] = phi[i] * prime[j];
				break;
			}
			phi[i * prime[j]] = phi[i] * phi[prime[j]];
		}
	}
}

欧拉定理（欧拉降幂）

欧拉定理

与欧拉函数紧密相关的一个定理就是欧拉定理。其描述如下：

若 $\gcd(a,m)=1$，则 $a^{φ(m)}\equiv1(\mod m)$。

扩展欧拉定理

$$a^b\equiv\begin{cases} a^{b\mod φ(p)},&\gcd(a,p)=1\\ a^b,&\gcd(a,p)\ne1,b<φ(p)\\ a^{b\mod φ(p)+φ(p)},&\gcd(a,p)\ne1,b\geφ(p) \end{cases}(\mod p) $$

数论分块

介绍

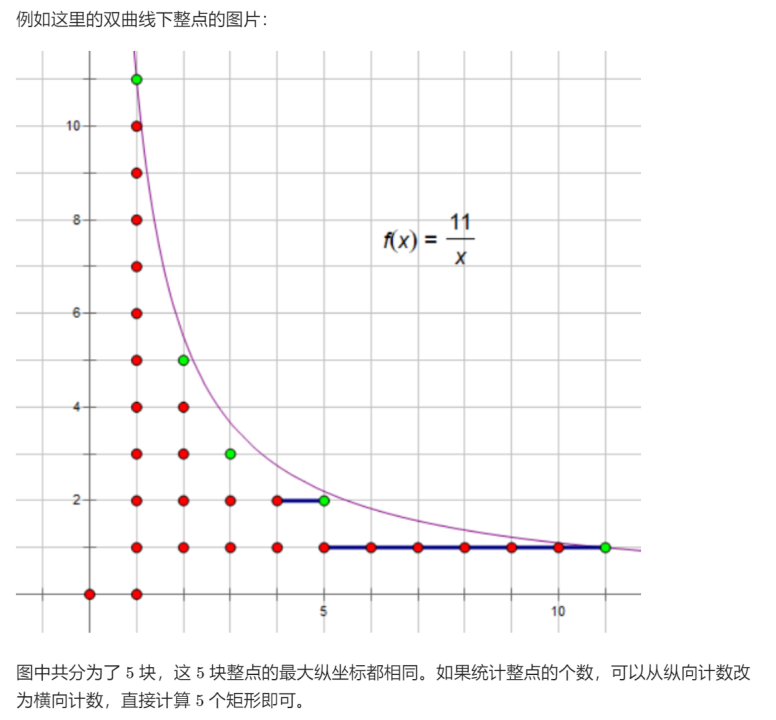
例子

原理

• 原理 1

• 原理 2

$\dfrac{n}{i}$ 最多只有 $2\sqrt{n}$ 种取值。

过程