青蛙

设经过s步后两青蛙相遇，则必满足该等式：(x+m* s)-(y+n* s)=k​l(k=0,1,2....)​ 将等式进行变形得：(n-m)s+kl=x-y 令n-m=a,k=b,x-y=c,即原式可以转换为：as+b*l=c 若上式存在整数解，则两青蛙能相遇，否则不能。

首先想到的一个方法是用两次for循环来枚举s,l的值，看是否存在s,l的整数解，若存在则输入最小的s，但显然这种方法是不可取的，谁也不知道最小的s是多大，如果最小的s很大的话，超时是明显的。

其实这题用欧几里德扩展原理可以很快的解决，先来看下什么是欧几里德扩展原理： 欧几里德算法又称辗转相除法，用于计算两个整数a,b的最大公约数。其计算原理依赖于下面的定理：gcd(a,b) = gcd(b,a mod b) 证明：a可以表示成a = kb + r，则r = a mod b 　　 假设d是a,b的一个公约数，则有d|a, d|b，而r = a - kb，因此d|r，所以d是(b,a mod b)的公约数 　　 假设d 是(b,a mod b)的公约数，则d | b , d |r ，但是a = kb +r，因此d也是(a,b)的公约数 　　 因此(a,b)和(b,a mod b)的公约数是一样的，其最大公约数也必然相等，得证

欧几里德算法就是根据这个原理来做的，其算法用C++语言描述为：

int Gcd(int a, int b)
{
    　　if(b == 0)
        　　return a;
    return Gcd(b, a % b);　　
}

也可以写成迭代的形式：

int Gcd(int a, int b)　
{
    while(b != 0)
    {
        int r = b;
        b = a % b;
        a = r;
    }
    return a;
}

补充: 扩展欧几里德算法是用来在已知a, b求解一组x，y使得a* x+b*y=Gcd(a,b)(解一定存在，根据数论中的相关定理)。扩展欧几里德常用在求解模线性方程及方程组中。下面是一个使用C++的实现：

int exGcd(int a, int b, int &x, int &y)　
{
    if(b == 0)
    {
        x = 1;
        y = 0;
        return a;
        　　
    }
    int r = exGcd(b, a % b, x, y);
    int t = x;
    x = y;
    y = t - a / b * y;
    return r;　　
}

把这个实现和Gcd的递归实现相比，发现多了下面的x,y赋值过程，这就是扩展欧几里德算法的精髓。 可以这样思考: 对于a' = b, b' = a % b 而言，我们求得 x, y使得 a'x + b'y = Gcd(a', b') 由于b' = a % b = a - a / b * b (注：这里的/是程序设计语言中的除法) 那么可以得到:a'x + b'y = Gcd(a', b') ===> 　　bx + (a - a / b * b)y = Gcd(a', b') = Gcd(a, b) ===> 　　ay +b(x - a / by) = Gcd(a, b) 因此对于a和b而言，他们的相对应的p，q分别是 y和(x-a/by). 　　 在网上看了很多关于不定方程方程求解的问题，可都没有说全，都只说了一部分，看了好多之后才真正弄清楚不定方程的求解全过程，步骤如下： 求a * x + b * y = n的整数解。 1、先计算Gcd(a,b)，若n不能被Gcd(a,b)整除，则方程无整数解；否则，在方程两边同时除以Gcd(a,b)，得到新的不定方程a' * x + b' * y = n'，此时Gcd(a',b')=1; 2、利用上面所说的欧几里德算法求出方程a' * x + b' * y = 1的一组整数解x0,y0，则n' * x0,n' * y0是方程a' * x + b' * y = n'的一组整数解； 3、根据数论中的相关定理，可得方程a' * x + b' * y = n'的所有整数解为： x = n' * x0 + b' * t y = n' * y0 - a' * t (t为整数) 上面的解也就是a * x + b * y = n 的全部整数解。

扩展欧几里得

实现1

实现2

分析扩展欧几里得得到的解

乘法逆元

方法1 扩展欧几里得

方法2 费马小定理

性质

特定数的逆元

• 1的逆元
• 2的逆元

威尔逊定理证明

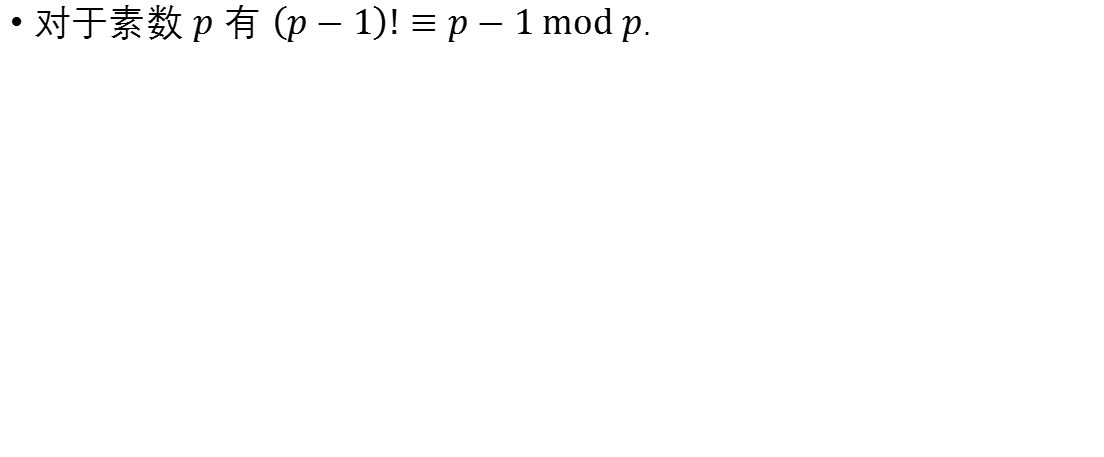
逆元扩展

• 线性求逆元
• 线性求阶乘逆元
• 线性求任意n个数逆元