引入

• 单模式串匹配问题：懒得写直接点这个。
• 多模式串匹配问题：给定一个由 $n$ 个模式串 $t_i$ 组成的字典，和文本串 $s$：多少个模式串 $t_i$ 串在文本串 $s$ 中出现过。 如：$s=$ abababc，$t=$ {aba,bc}，则所有出现位置为 $1$、$3$ 和 $6$。
  • KMP： 将问题看做是：每个字典串与询问串的单模式串匹配。 字符串相互独立，没有打通链路，充分利用字典串之间的关系，导致时间复杂度很高（$\mathcal{O(n|s|+\sum\limits_{i=1}^n|t_i|)}$）。
  • Trie： 利用字典树进行多模式的匹配。 不能够在失配时进行合理的跳转，盲目尝试，导致复杂度很高（$\mathcal{O(\sum\limits_{i=1}^n|t_i|+|s|\times\max\limits_{i=1}^nt_i)}$）。

AC 自动机

概念

• AC 是两个人名字的首字母，AC 自动机 $=\texttt{Aho-Corasick\ automation}\ne$ 自动 AC 机。
• AC 自动机 =KMP+Trie。 基于 $Trie$，将 KMP 的 $\texttt{Border}$ 概念推广到多模式串上。
• 是一种离线型数据结构，即不支持增量添加新的模式串（同前缀和）。
• 常用于将字符串询问类的问题进行离线处理，也经常与各种 dp 结合。
• 是 Automaton/Automata，不是自动化的那个自动，属于专有名词。

自动机（编译原理）

一般指确定有限状态自动机 DFA。

自动机指可以判定一个序列是否是某种特定序列的数学模型。

• 序列：字符串、数列
• 特定序列：回文串、是否是另一序列的子串/子序列、大整数能否被 $3$ 整除。如果一个序列被判定为该特定序列，则我们会说该序列被接受，否则会说不接受。
• 数学模型：不是一种算法和数据结构，可以有不同的实现方式。

一般会体现为一个有向图。

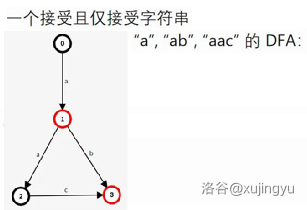
一些自动机 DFA

• DFA 一般有五个要素组成，以字典树（可以接受在字典里的字符串）为例：

  • 字符集：小写字母（大写字母），该自动机只能输入这些字符。
  • 状态：即为树上的顶点，树的顶点数量有限（有限状态）。
  • 起始状态为根节点（空串）。
  • 接收状态集合（有特定标记的树节点）
  • 转移函数：树边，每条边上有一个字符，而且每个点的字符

• 序列自动机

构建

构建 AC 自动机统共分两步：

1. 基础的 Trie 结构：将所有的模式串构成一棵 Trie；
   • I he his she hers
2. KMP 的思想：为 Trie 树上所有的节点构造失配指针。
   • 回忆一下KMP 的流程：
   • 每次失配的时候，往最大 $\texttt{Border}$ 跳，即往 $next$ 指针跳。
   • KMP 指针一定是往前指的。
   • 考虑在字典树上暴力匹配的过程。

Border 概念的推广

• 广义 $\texttt{Border}$
• 推广到两个串：对于两个串 $s$ 和 $t$，相等的 $p$ 长度 $s$ 的后缀和 $t$ 的前缀称为一个 $\texttt{Border}$。
• 推广到一个字典：对于串 $s$ 和一个字点 $d$，相等的 $p$ 长度的 $s$ 的后缀，和任意一个字典串 $t$ 的前缀称为一个 $\texttt{Border}$。
• 失配（Fail）指针：对于 Trie 中的每一个节点（即某个字典串的前缀），它与 Trie 中所有串的最大 $\texttt{Border}$ 即为失配指针。

AC 自动机

• 失配指针
• 类似与 KMP 求 $\texttt{Border}$，任意节点的 $\texttt{Border}$ 的父节点对应的字符串，一定是父节点的 $\texttt{Border}$。因此可以通过遍历父节点的失配指针链来求解。
• 因此在求失配指针的时候，一定要按长度从小到大来就，即 bfs。

例子：

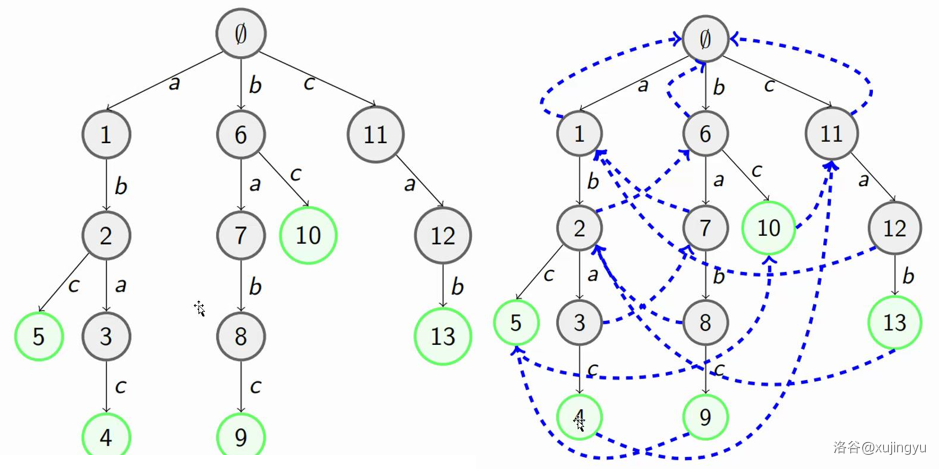
主要步骤

这。