评价：

$\textrm{It\ was\ so\ fucking\ niubility\ that\ I\ can\ only\ say\ that\ orz.}$

回文串

• 设 $R(s)$ 为 $s$ 相反的串，即若 $s=R(s)$，该串回文。

• 回文中心：

  • 奇（长度）回文串，回文中心为 $s_{\frac{n+1}{2}}$，如 abcba；
  • 偶（长度）回文中心为 $s_\frac{n}{2}$ 与 $s_{\frac{n}{2}+1}$ 中间，如 abc|cda。

• 回文半径 $L$：回文中心到回文串左右端点到距离相等，此距离成为回文半径。

  • 如 abcba 半径为 $3$；
  • abcd|dcba 半径为 $4$。

• 常用二元组 $\text{<回文中心,回文半径>}$ 来表示一个回文子串。

回文串的性质

• 长度与半径的关系：
  • 奇回文串：$|s|=2L-1$；
  • 偶回文串：$|s|=2L$。
• 回文半径到单调性：回文半径 $-1$ 等价于同时删掉回文串的首尾字母，依然是回文串。
• 回文串的 $\texttt{Border}$：对于回文串 $s$，回文串前（后）缀等价于 $\texttt{Border}$。例子：abacaba。

求回文子串

给出一个字符串 $s$，求 $s$ 每个回文中心（包含每个字符作为中心和每两个字符中间作为中心）对应的回文半径。

二分 + 哈希

• 利用回文半径到单调性，预处理 $s$ 和 $R(s)$ 的 Hash，然后利用二分 +Hash 求每个中心的回文半径。复杂度 $\mathcal{O(n\log n)}$。但是没有考虑到不同回文中心之间的联系，如 abacaba，$s<2,2>$、$s<4,4>$ 均为回文子串，不需要计算我们就可得知 $s<6,2>$ 也为回文子串。

Manacher

前期处理：

• 为了将偶回文串的处理方式与奇回文串统一起来，将 $s$ 的每两个字母中间，以及开头结尾插入 #。例如 $s=$ bccbeb，预处理后变为 $s^{\#}=$ #b#c#c#b#e#b。因此所有回文串都变为奇数长度，且首尾一定是 #，例如：
  • 原始偶回文串：bccb$^{\#}=$ #b#c#c#b#，长度是 $9$，回文中心是 #；
  • 原始奇回文串：beb$^{\#}=$ #b#e#b#，长度是 $7$，回文中心是 e；
• 同时，所有极长回文子串长度一定为奇数：因为极长回文子串一定以 # 开头结尾。
• 容易发现：$|s^{\#}|=2|s|+1$，以及 $|s|=\dfrac{|s^{\#}|-1}{2}=\lfloor\dfrac{|s^{\#}|}{2}\rfloor$。
• 而 $s^{\#}$ 的回文半径为 $\dfrac{|s^{\#}|+1}{2}=|s|+1$。

过程：

• 定义 $len_i$ 表示以 $i$ 为回文中心的最大回文半径。
• 最右回文子串 $p$：所有已求得的回文子串中，右端点最靠右的一个。同样用两个参数描述：
  • $p_c$ 该回文子串的回文中心；
  • $len_{p_c}$ 该回文子串的回文半径长度。
• 根据上文，实际上 $len_{p_c}-1$ 就是以 $p_c$ 为回文中心的回文子串的长度，如下表所示，考虑字符串 abaaba：

i	0	1	2	3	4	5	6	7	8	9	10	11	12	13
str	$	#	a	#	b	#	a	#	a	#	b	#	a	#
len	1		2	1	4	1	2	7	2	1	4	1	2	1

• 暴力求 $len$ 数组：暴力枚举每个点，往外扩展

for(int i = 1;i < n;i++)
{
	len[i] = 1;
	while(str[i + len[i]] == str[i - len[i]]) len[i]++;
}

流程：

从左到右求每个位置的回文半径，同时维护当前最右回文子串回文中心 $p_c$ 及其右端点 $R=p_c+len_{p_c}-1$（当前最右回文子串的左端点即为 $L=p_c-len_{p_c}+1$），最右回文子串可以用 $s_{L,R}$ 来表示。

设当前 $1,2,\dots,i-1$ 位置的 $len$ 已经求出，当前需求 $len_i$，显然此时必然有 $p_c<i\leq R+1$

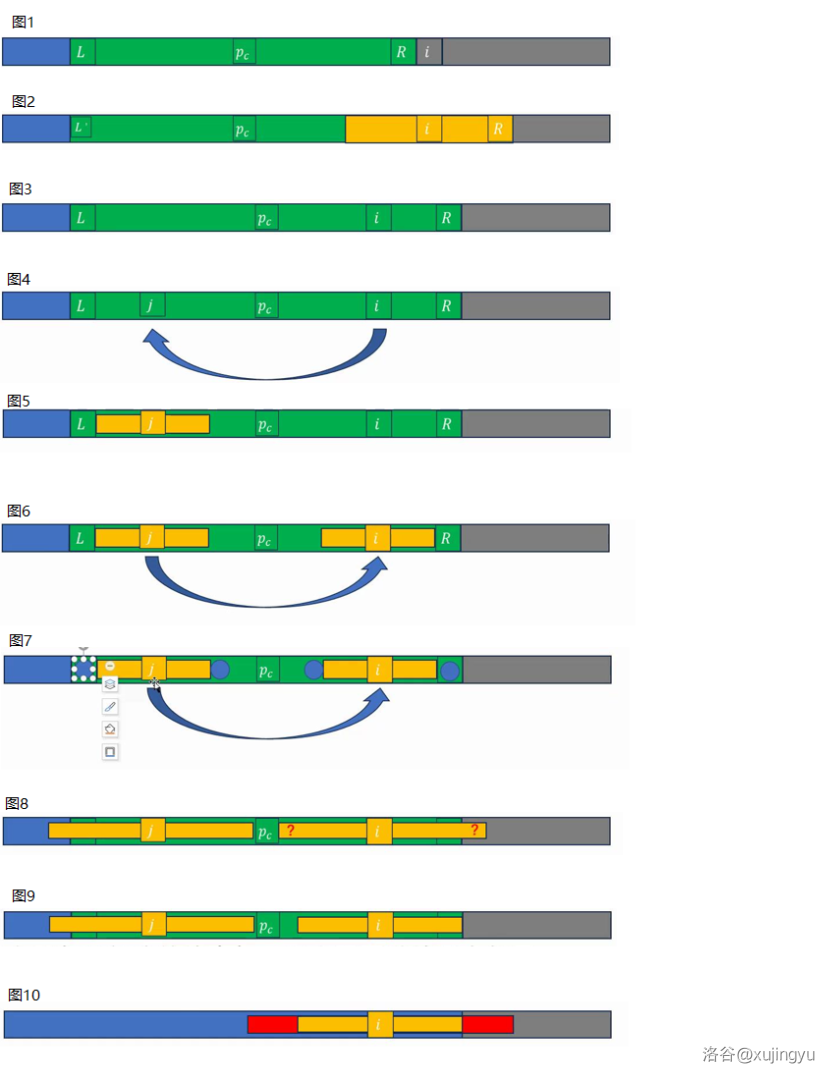
根据 $i$ 与 $R$ 的关系，总共分三类情况讨论：

1. $i>R$

   图1^[1]；

   以 $i$ 为回文中心，向左向右暴力拓展，求得回文半径 $len_i$，同时最右回文串会变为：

   • $p_c=i$；
   • $L=i-len_i-1$；
   • $R=i+len_i-1$；

   图2^[1:1]

2. $i\leq R$

   图3^[1:2]

   • 由于回文串的对称性：最右回文串 $p$ 的左半右半是对称的，找到 $i$ 关于 $p_c$ 的对称位置 $j=2p_c-i$。

     图4^[1:3]

   • 由于 $len_j$ 已知，根据最右回文串的对称性，$len_i$ 可以直接继承 $len_j$ 在最右回文串范围内的部分，根据 $len_j$ 是否超出了最右回文串的范围，继续讨论两种情况。

     1. $len_j$ 在 $p$ 的范围，即 $j-len_j+1>L$

        图5^[1:4]

        由于 $len_j$ 没有超出最右回文串的表示范围，由对称性，可以确定 $len_i=len_j$，且不能够再拓展。

        图6^[1:5]

        此时，最右回文串没有发生变化。

        图7^[1:6]

     2. $j-len_j+1\leq L$

        图8^[1:7]

        由于 $len_j$ 超出了最右回文串的范围，且灰色部分的值未知，因此 $len_i$ 至多只能集成到最右回文串范围内的 $len_j$，即 $len_i=j-L+1$。

        图9^[1:8]

        之后由于灰色部分未知，因此需要继续暴力拓展。

        图10^[1:9]

        当然，最右回文串会更新 $i$。

复杂度分析和应用

• 复杂度分析：每次暴力匹配一定伴随着最右回文串右端点 $R$ 的右移。因此复杂度为线性。
• 代码：

string str;
char s[2000001];//注意要开两倍大小
int len[2000001],maxn;

void Manacher(string a,int n)
{
	//插入#字符
	int l = 0;
	s[0] = '$';//放一个必然不存在的字符,省去判断有没有出界
	s[1] = '#';
	for(int i = 0;i < n;i++)
	{
		s[2 * i + 2] = a[i];
		s[2 * i + 3] = '#';
	}
	n = n * 2 + 2;
	s[n] = 0;
	int pc = 0,R = 0;
	for(int i = 1;i < n;i++)
	{
		if(i > R) len[i] = 1;
		else
		{
			int L = pc - len[pc] + 1;
			int j = pc * 2 - i;
			if(j - len[j] + 1 > L) len[i] = len[j];
			else len[i] = j - L + 1;
		}
		//暴力扩展
		//第2种情况j-len[j]+1>L不需要暴力扩展
		//但是也不影响,因为不可能会发生扩展
		while(s[i + len[i]] == s[i - len[i]]) len[i]++;
		//更新最右回文子串
		if(i + len[i] - 1 > R)
		{
			R = i + len[i] - 1;
			pc = i;
		}
	}
	return;
}

应用：

每个回文中心的回文半径；

求本质不同回文子串：

• 对于字符串 $s$，如果它的两个子串 $s_1$、$s_2$ 均为回文串且 $s_1\ne s_2$，则称它们是本质不同的。例如：abacaba 一共有七个本质不同的回文子串。
• 一个串本质不同的回文子串最多只有 $n$ 个。

在 Manacher 中，新的回文串一定出现在使得最右串右移的时候。因此本质不同的回文串最多 $n$ 个。把所有更新最右回文串去重即得到本质不同回文串。

Link

扩展知识

回文自动机

• 前置知识：

  • Manacher（不完全需要，会能更加理解回文串相关性质）；
  • AC 自动机（需要非常熟悉）。

• 原理： 回文串的 $\texttt{Border}$ 必然也是一个回文串；

  反之亦然：回文串的回文后缀必然是它的 $\texttt{Border}$。

---

1. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎