$\textrm{Cannot\ get\ hitokoto.}$

状态压缩 dp

状压 DP 是动态规划的一种，通过将状态压缩为整数来达到优化转移的目的。

状态压缩

状态压缩 dp 就是状态表示比较复杂的一种 dp，不像序列 dp，树形 dp，之类的直接 $dp_i$ 表示 $i$ 这个前缀，或者 $i$ 这个子树的相关信息。

状压 dp 要求表示的状态往往是一个集合的一个子集，一张图的一个子图，需要你手动把这些状态和整数之间建立起一个一一对应关系，简单地说，就是状态压缩。

例如：取或不取，砝码放左边、右边或者不拿，排列康托展开。

内容

最常见的状压 dp 是子集 dp，也即有一个集合 $s=\{0,1,\dots,n-1\}$，一个状态是 $s$ 的一个子集。这时一般用一个二进制数 $x$ 来表示 $s$ 的一个子集。如果 $x$ 对应位上是 $1$ 就表示该数在子集内，否则不在。

比如 $10110$ 表示一个大小为 $5$ 的集合，第 $1$、$2$、$4$ 个在当前子集中（最右边下标为 $0$，往左递增）。

位运算

需要熟悉位运算：

• &：取交集；
• | 取并集；
• ~ 取补集；
• ^ 对称差；
• <<>> 左移右移，做一些特殊的操作；
• x>>i&1 取出第 $i$ 位；
• x&(-x)：能整除这个数的最大的二的幂。

若当前状态为 $s$，对 $s$ 有下列操作：

1. 判断第 $i$ 位是否为 $0$：(s&1<<i)==0；
2. 将第 $i$ 位设置为 $1$：s|=1<<i；
3. 将第 $i$ 位设置为 $0$：s&=~(1<<i)。

例如：$s=1010101$，$i=5$：

1. $=0$；
2. $=1110101$；
3. $=1010101$。

例1：铺砖问题

题目。

$n$ 比较小时可以考虑搜索，如果采用宽搜，每一个点都有两种铺法，因此可以扩展出两个节点，要求所有的点，必须扩展全部树结构。

$n$ 比较大时需要考虑其他方法。

• 性质1：如果 $w$ 和 $h$ 都是奇数，则无解，否则有解；
• 性质2：对于每铺一次地板，只会影响所铺的上下行；
• 性质3：如果按行铺地板，每一行的铺法都类似。

一个 $6\times9$ 的铺法如下图：

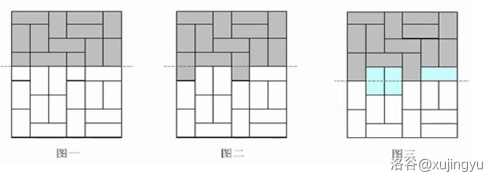
可以看出，在按行铺的过程中，某些砖会分成两半，如图 2，但最多也是向下突出一格，在图 3 中，我们将图 2 的空隙填满，则又转移到了下一种状态。

用一个整数表示铺砖状态，若某格被铺了砖，则用 1 表示，没有铺砖，则用 0 表示，那么行的状态就是一个 $w$ 位 01 串，即 $w$ 位的二进制数，如下图状态为：100100。

灰	白		灰	白

（脑补）

那么如何转移：考虑每个空缺位置怎么放砖，一共有两种方法，那么考虑将第 $i-1$ 行的空位填满的情况下，$i$ 行的状态，比如 $100100$ 可以变为 $011011$、$011000$、$000000$ 等。

那么怎么知道每个状态由哪些状态转移得到呢。

可以用 dfs 暴力 check 每个状态怎么转移：

对于第 $i$ 行的状态 $s$，它是由 $i-1$ 行的状态 $s'$ 转化过来的，显然，对于该行某个位置 $j$：

• 如果 $i-1$ 行该位置为 $0$，那么该位置可以竖放，即 $0→1$；
• 如果 $i-1$ 行连续两个位置为 $0$，那么这两个连续位置可以横放，即 $00→00$；
• 如果 $i-1$ 行该位置为 $1$，显然该位置不能再放，于是应该把该位置设置为 $0$，即 $1→0$。

#include <bits/stdc++.h>
using namespace std;

int n,m,p,dp[20001][32];

void dfs(int h,int k,int s,int ss)//第i行要铺第k列,第i+1行状态为s,第i行状态为ss
{
	if(k >= m){dp[h + 1][s]=(dp[h + 1][s] + dp[h][ss]) % p;return;}
	if(!(ss & (1 << k)))
	{
		dfs(h,k + 1,s ^ (1 << k),ss);//竖铺,只有此时会影响下一行
		if(k < m - 1 && (!(ss & (1 << k + 1)))) dfs(h,k + 2,s,ss);//横铺，判断下一行有没有铺过
	}
	else dfs(h,k + 1,s,ss);
	return;
}

signed main()
{
	scanf("%d%d%d",&n,&m,&p);
	dp[1][0] = 1;
	for(int i = 1;i <= n;i++)
	for(int j = 0;j <= (1 << m) - 1;j++)
	dfs(i,0,0,j);//dfs枚举的是铺完第i行能够将第i+1行铺成的状态
	printf("%d",dp[n + 1][0]);
    return 0;
}

例2：棋盘问题

题目。

设：

• $dp_{i,j,l}$ 表示对于前 $i$ 行，第 $j$ 种状态，$l$ 个国王的方案数；
• $sit_j$ 表示第 $j$ 种状态，例如第 $5$ 种状态是 101（1 表示当前格放国王），那么 $sit_5=5$；
• $sta_j$ 表示第 $j$ 种状态下的国王数；
• $x$ 表示上一行状态。

易得 $dp_{i,j,l}=\sum\limits_{i=2}^n dp_{i-1,x,l-sta_j}$。

判断一个国王下面是否有国王，直接将 sit[j] & sit[x]，若为 $1$ 就说明有；左下和右下只需左移即可。

#include <bits/stdc++.h>
#define int long long
using namespace std;

int n,k,sit[2001],sta[2001],tot,dp[11][2001][101],sum;

void dfs(int x,int cnt,int pos)//得到每个状态
{
	if(pos >= n)
	{
		sit[++tot] = x;
		sta[tot] = cnt;
		return;
	}
	dfs(x,cnt,pos + 1);//取0
	dfs(x + (1 << pos),cnt + 1,pos + 2);//取1
	return;
}

signed main()
{
	scanf("%lld%lld",&n,&k);
	dfs(0,0,0);
	for(int i = 1;i <= tot;i++) dp[1][i][sta[i]] = 1;
	for(int i = 2;i <= n;i++)
	{
		for(int j = 1;j <= tot;j++)
		{
			for(int x = 1;x <= tot;x++)
			{
				if((sit[j] & sit[x]) || ((sit[j] << 1) & sit[x]) || (sit[j] & (sit[x] << 1)))continue;
				for(int l = sta[j];l <= k;l++) dp[i][j][l] += dp[i - 1][x][l - sta[j]];
			}
		}
	}
	for(int i = 1;i <= tot;i++) sum += dp[n][i][k];//累加
	printf("%lld",sum);
	return 0;
}