树链剖分

序列维护

给出一个序列，维护以下操作：

1. 区间修改；
2. 区间查询。

做法：线段树。

树上信息维护

给出一棵树，维护以下操作：

1. 链上修改；
2. 链上查询；
3. 子树修改；
4. 子树查询。

做法：暴力树链剖分。

树链剖分

用于维护上述信息的一种数据架构。

将一棵树划分成若干条链，用数据结构去维护每条链，通常结合线段树来使用。

剖分方法：

• 盲目剖分；
• 随机剖分；
• 启发式剖分。

按拆分的决策：

• 重链剖分；
• 长链剖分；
• 实链剖分（Link/cut Tree）。

相关概念

• $size(u)$：以 $u$ 为根的子树的节点个数。
• 重儿子 $son(u)$：一个节点的子节点中，$size$ 最大的那个子节点。
• 轻儿子：非重儿子的其他子节点。
• 重边：一个点到它的重儿子的边。
• 轻边：一个点到它的轻儿子的边。
• 重链：由重边连结形成的链。

一个非叶节点有且仅有一个重儿子。

轻重链剖分性质

一条链可以被拆分成不超过 $\mathcal{O(\log n)}$ 条重链。

只需要证明一个点到根的路径上有不超过 $\mathcal{O(\log n)}$ 条重链。

点到根的路径为重链和轻边交错，因此只需要证明有不超过 $\mathcal{O(\log n)}$ 条轻边就行了。

沿着父节点指针往上走，如果走过一条轻边，因为这是轻边，所以父节点一定有个重儿子比当前儿子大，换句话说：

$$size_{fa_x}>size_x\times2$$

又 $size_{root}=n$，故用线段树维护一条链的复杂度不超过 $\mathcal{O(\log^2n)}$。

dfs 序

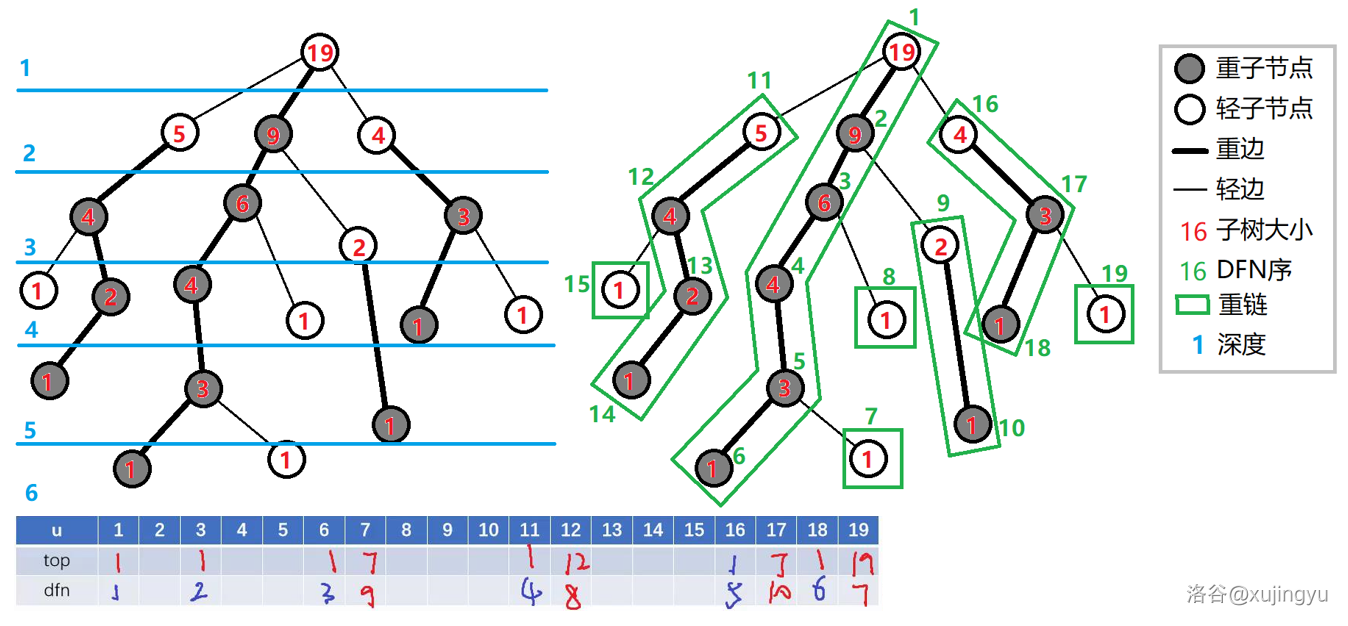
从根节点开始深搜，一个点向下深搜的时候优先搜重儿子，得到一个 dfs 序。

容易发现，这样得到的 dfs 序中一条重链中的点是按照深度从小到大的顺序排在一起的。

一条链可以被拆分为一些重链的并，每条重链都是 dfs 序上的一个区间，因此一条链就可以拆分成序列上的一些区间。

由于是 dfs 序，所以一个节点的子树在 dfs 序上是一段区间。

这样链和子树就都转化成了序列上的区间。

通常使用线段树来维护区间。

实现

重链剖分的过程为 $2$ 次 dfs。

• 第一次：找重儿子、重边；
• 第二次：连重边成重链。

找重边

第一次 dfs，对于每个点 $u$，记下其 $size$ 值最大的儿子节点 $son(u)$，也即所有的重边，以及其它需要记录的量（父节点，深度，$siz$）。

void dfs1(int u,int f)
{
	son[u] = -1;
	siz[u] = 1;
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		if(v == f) continue;
		dep[v] = dep[u] + 1;
		fa[v] = u;
		dfs1(v,u);
		siz[u] += siz[v];
		if(son[u] == -1 || siz[v] > siz[son[u]]) son[u] = v;
	}
	return;
}

连重边成重链

第二次 dfs，以根节点为起点，沿重边向下拓展，拉成重链。

不在当前重链上的节点，都以该节点为起点向下重新拉一条重链。

记录 top 数组和 dfs 序（以及逆数组 rnk）。

int top[101],dfn[101],rnk[101],tot;

void dfs2(int u,int t)
{
	top[u] = t;
	tot++;
	dfn[u] = tot;
	rnk[tot] = u;
	if(son[u] == -1) return;
	dfs2(son[u],t);//优先对重儿子进行dfs,可以保证同一条链上的点dfs序连续
	for(int i = 0;i < g[u].size();i++)
	{
		int v = g[u][i];
		if(v == son[u] || v == fa[u]) continue;
		dfs2(v,v);
	}
	return;
}

基础应用

1. 查询两个点 $u$，$v$ 的 LCA。

• 如果 $u$，$v$ 在同一重链上，则 lca 为两者中深度 $dep$ 更小的那个。
• 否则假设 $v$ 深度 $dep$ 更大，则将 $v$ 往上跳一次重链 $v=fa_{top_v}$。

int lca(int u,int v)
{
	while(top[u] != top[v])
	{
		if(dep[top[u]] > dep[top[v]]) u = fa[top[u]];
		else v = fa[top[v]];
	}
	return dep[u] > dep[v]?v:u;
}

2. 单独修改一个点的权值：根据新的编号直接在数据结构中修改就行了。
3. 查询两个点之间的距离：查询链的时候，对于一条 $u$ 到 $v$ 的链，讨论：
   • 若 $u$ 和 $v$ 在同一条重链上，那么 $u$ 到 $v$ 的链在 dfs 序上是一段区间，直接去线段树上查询；
   • 否则，不妨设 $dep_{top_u}>dep_{top_v}$，去线段树上查询 $u$ 到 $top_u$ 这段链对应的区间，然后把 $u$ 改为 $fa_{top_u}$，重复上述过程。

例题

题目

#include <bits/stdc++.h>
using namespace std;

int n,m,a[30001],dep[30001],fa[30001],siz[30001],son[30001],top[30001],dfn[30001],rnk[30001],sum[120001],maxn[120001],w[30001];
string op;
vector <int> g[30001];

void dfs1(int u)
{
    siz[u] = 1;
    for(int i = 0;i < g[u].size();i++)
    {
    	int v = g[u][i];
        if(v == fa[u]) continue;
        fa[v] = u;
		dep[v] = dep[u] + 1;
		dfs1(v);
        if(siz[son[u]] < siz[v]) son[u] = v;
        siz[u] += siz[v];
    }
    return;
}

void dfs2(int u,int tp)
{
    dfn[u] = ++dfn[0];
    top[u] = tp;
    w[dfn[0]]=a[u];
	if(!son[u]) return;
	dfs2(son[u],tp);
	for(int i = 0;i < g[u].size();i++)
    {
    	int v = g[u][i];
        if(v == fa[u] || v == son[u]) continue;
		dfs2(v,v);
    }
    return;
}

void build(int p,int l,int r)
{
    if(l == r) {sum[p] = maxn[p] = w[l];return;}
    int mid = l + r >> 1;
    build(p << 1,l,mid);
	build(p << 1 | 1,mid + 1,r);
    sum[p] = sum[p << 1] + sum[p << 1 | 1];
    maxn[p] = max(maxn[p << 1],maxn[p << 1 | 1]);
    return;
}

void change(int p,int l,int r,int u,int val)
{
    if(l == r){sum[p] = maxn[p] = val;return;}
    int mid = l + r >> 1;
    if(u <= mid) change(p << 1,l,mid,u,val);
    else change(p << 1 | 1,mid + 1,r,u,val);
    sum[p] = sum[p << 1] + sum[p << 1 | 1];
    maxn[p] = max(maxn[p << 1],maxn[p << 1 | 1]);
    return;
}

int ask_sum(int p,int l,int r,int u,int v)
{
    if(u <= l && r <= v) return sum[p];
    int mid = l + r >> 1,ans = 0;
    if(u <= mid) ans = ask_sum(p << 1,l,mid,u,v);
    if(v > mid)ans += ask_sum(p << 1 | 1,mid + 1,r,u,v);
    return ans;
}

int ask_max(int p,int l,int r,int u,int v)
{
    if(u <= l && r <= v) return maxn[p];
    int mid = l + r >> 1,ans = -30000;
    if(u <= mid) ans = ask_max(p << 1,l,mid,u,v);
    if(v > mid) ans = max(ans,ask_max(p << 1 | 1,mid + 1,r,u,v));
    return ans;
}

int query_max(int u,int v)
{
    int fu = top[u],fv = top[v],ans = -30000;
    while(fu != fv)
    {
        if(dep[fu] < dep[fv]){swap(u,v);swap(fu,fv);}
        ans = max(ans,ask_max(1,1,n,dfn[fu],dfn[u]));
        u = fa[fu],fu = top[u];
    }
    if(dep[u] > dep[v]) swap(u,v);
    ans = max(ans,ask_max(1,1,n,dfn[u],dfn[v]));
    return ans;
}

int query_sum(int u,int v)
{
    int fu = top[u],fv = top[v],ans = 0;
    while(fu != fv)
    {
        if(dep[fu] < dep[fv]){swap(u,v);swap(fu,fv);}
        ans += ask_sum(1,1,n,dfn[fu],dfn[u]);
        u = fa[fu];
		fu = top[u];
    }
    if(dep[u] > dep[v]) swap(u,v);
    ans += ask_sum(1,1,n,dfn[u],dfn[v]);
    return ans;
}

signed main()
{
    scanf("%d",&n);
    for(int i = 1;i < n;i++)
    {
    	int u,v;
		scanf("%d%d",&u,&v);
		g[u].push_back(v);
		g[v].push_back(u);
	}
    for(int i = 1;i <= n;i++) scanf("%d",&a[i]);
    dfs1(1);
	dfs2(1,1);
	build(1,1,n);
    scanf("%d",&m);
    while(m--)
    {
    	int u,v;
    	cin >> op;
        scanf("%d%d",&u,&v);
        if(op == "CHANGE") change(1,1,n,dfn[u],v);
        else
		{
            if(op == "QMAX") printf("%d\n",query_max(u,v));
            else printf("%d\n",query_sum(u,v));
        }
    }
    return 0;
}