常用概念 几何概型

• 为了简化概念，此处只涉及有限的样本空间和离散的事件。
• 基本事件：不可再分割，随机变量的某个取值，也叫样本点 $𝜔$ 比如单次投掷出 $5$ 即为基本事件
• 事件 $𝐸$：基本事件的某个集合体 比如投掷结果为偶数
• 样本空间 $Ω$：所有的基本事件 比如投掷一个骰子得到的所有可能结果构成样本空间
• 示性函数 $𝐼_𝐴$：如果得到的结果是事件 $𝐴$，则该值为 $1$，否则为 $0$。

概率

概率本质上就是从事件到一个实数值的函数，通常记作 $𝑃$。概率必须满⾜三个条件：

• （非负性）对任意事件 $𝐴$ 都有 $𝑃(𝐴)\leq0$；
• （正规性）$𝑃(Ω)=1$；
• （可加性）如果事件 $𝐴_1,𝐴_2,\dots$ 两两互斥，那么 $𝑃(ڂ𝐴_𝑖)=\sum𝑃(𝐴_𝑖)$。
  • 互斥事件：发生 $𝐴$ 则不可能发生 $𝐵$，则称事件 $𝐴$ 和 $𝐵$ 互斥（今天是周四与今天是周五）；
  • 对立事件：$𝐴$ 和 $𝐵$ 互斥，且要么 $𝐴$，要么 $𝐵$（今天是周五和今天不是周五）。

概率的解释

概率的解释到现在都是一个有争议的话题。学者分为两派：

• 频率学派：认为概率是相对频数的极限，是一种客观属性。这其 实是⼤多数⼈一开始接触概率时的看法。这一说法适⽤于可以反复观测的事件，随着观测次数趋于⽆穷，事件发生的相对频数会 越来越趋近于真正的概率。如掷骰子。
• ⻉叶斯学派：认为概率描述的是信⼼的程度，带有一些主观的成 分。比如，可以说“明天下⾬的概率是 $90\%$”，但显然我们⽆法多次 观测这一事件。这⾥的 $90\%$ 代表我们对于“明天下⾬”这一事件的信⼼，将来如果我们得到的新的数据（比如云层的变化），我们可 能会对这一信⼼进⾏修正。

独⽴事件与条件概率

• 独立：对于事件 $𝐴$ 和 $𝐵$，如果 $𝑃(𝐴𝐵)=𝑃(𝐴)𝑃(𝐵)$，那么称 $A$ 和 $B$ 是独立的。（注：$𝐴𝐵$ 表示 $𝐴$ 和 $𝐵$ 的交集，$𝐴+𝐵$ 表示两者的并集） 所谓独立，即一次实验中一事件的发生不会影响到另一事件发生的概率。 例如一般连续两次掷骰子得到的点数结果是相互独立的。
• 条件概率：如果 $𝑃(𝐵)>0$，那么 $𝐴$ 在 $𝐵$ 下的条件概率为 $P(𝐴|𝐵)=\dfrac{𝑃(𝐴𝐵)}{𝑃(𝐵)}$ 即，已知 $B$ 发生，在此前提下 $𝐴$ 发生的概率是多少。特别地，如果 $A$ 与 $𝐵$ 独立，那么 $𝑃(𝐴|𝐵)=𝑃(𝐴)$。 如 $B$ 是骰子投到偶数，$A$ 是投到 $2$。根据公式就是 $\dfrac{1}{3}$。

全概率公式

全概率公式：如果样本空间可以被划分为两两互斥的若⼲部分 $A_1,\dots,𝐴_𝑘$，即 $𝐴_1+𝐴_2+\dots+𝐴_𝑘=Ω$，那么 $𝑃(𝐵)=\sum\limits_{𝑖=1}^k𝑃(𝐵|𝐴_𝑖)𝑃(𝐴_𝑖)$。

全概率公式⽤于将不好算的事件拆分成若⼲个⼩的事件，分别计算。

⻉叶斯公式

公式

⻉叶斯公式：对于事件 $𝐴$ 和 $𝐵$，如果 $𝑃(𝐴)>0$ 且 $𝑃(𝐵)>0$，那么 $P(𝐴|𝐵)=\dfrac{𝑃(𝐵|𝐴)𝑃(𝐴)}{𝑃(𝐵)}$。

通常我们会有样本空间的一个划分 $𝐴_1,\dots,𝐴_𝑘$，结合全概率公式， 对于任意 $1\le 𝑖\le 𝑘$ 有：

$$P(𝐴_𝑖|𝐵)=\dfrac{𝑃(𝐵|𝐴_𝑖)𝑃(𝐴𝑖)}{P(B)}\\ P(𝐴_𝑖|𝐵)=\dfrac{𝑃(𝐵|𝐴_𝑖)𝑃(𝐴𝑖)}{\sum\limits_{j=1}^kP(B|A_j)P(A_j)} $$

⻉叶斯公式的解释

⻉叶斯公式其实是条件概率公式的直接推论。它描述的是这样的事实：

• $𝐴_𝑖$ 是我们想要描述的事件，如“某物体属于哪一类”。我们称 $𝑃(𝐴_𝑖)$ 为先验概率，代表我们一开始对物体类别分布的估计。
• $𝐵$ 是我们的一次观测，我们想利⽤观测的结果来对概率进⾏修正。 修正的结果 $𝑃(𝐴_𝑖|𝐵)$ 被称为后验概率。
• $𝑃(𝐵|𝐴_𝑖)$ 被称为似然函数。我们可以根据历史数据求得这一值。

⻉叶斯公式的应用：垃圾邮件识别

我们可以利⽤⻉叶斯公式做一个简单的⼩程序来识别垃圾邮件。

所有邮件分为两类：$𝐴_1$ 代表垃圾邮件，$𝐴_2$ 代表非垃圾邮件。根据经验，$𝑃(𝐴_1)=0.7$，$𝑃(𝐴_2)=0.3$。（先验概率）

令 $𝐵$ 表示邮件包含“免费”这一关键词，由历史邮件得知，$P(𝐵|𝐴_1)=0.9$，$𝑃(𝐵|𝐴_2)=0.01$（似然函数，注意：它们之和无意义且并不一定等于 $1$）。

新收到一封邮件，其中包含了“免费”词汇，它是垃圾邮件的概率是：

$$𝑃(𝐴_1|𝐵)=\dfrac{0.9\times0.7}{(0.9\times0.7)+(0.01\times0.3)}≈0.995 $$

三门问题

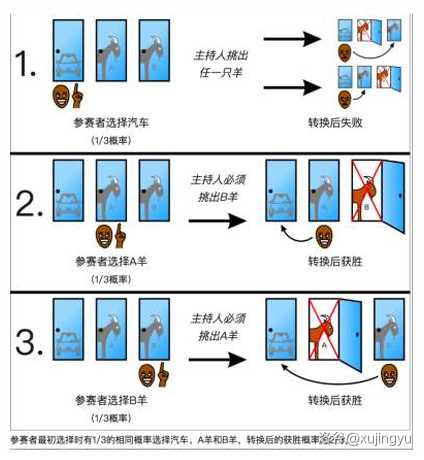
有三扇⻔，其中一扇⻔背后有奖⾦，剩下两扇背后什么也没有。 你选择了其中一扇⻔，此时主持⼈从剩下的两扇⻔中选择了一扇打开，后⾯什么也没有。此刻你是否应当更改选择另一扇没开的⻔？

直觉似乎是改不改⽆所谓，但我们可以⽤⻉叶斯的理论计算一下。

不妨设你选择的⻔是第 $1$ 扇，主持⼈打开的是第 $3$ 扇。设每扇⻔后⾯有奖⾦的事件为 $𝐴_𝑖$，那么先验概率为 $𝑃(𝐴_𝑖)=\dfrac{1}{3}$，我们想知道的是 $𝑃(𝐴_1|\overline{𝐴_3})$ 是多少。根据⻉叶斯公式有：

$$𝑃(𝐴_1|\overline{𝐴_3})=\dfrac{𝑃(\overline{𝐴_3}|A_1)P(A_1)}{𝑃(\overline{𝐴_3}|A_1)P(A_1)+𝑃(\overline{𝐴_3}|A_2)P(A_2)+𝑃(\overline{𝐴_3}|A_3)P(A_3)} $$

其中：

• 如果奖⾦在第 $1$ 扇⻔后⾯，主持⼈可以打开第 $2$ 或者第 $3$ 扇⻔，概率相同。因此 $𝑃(\overline{𝐴_3}|A_1)=\dfrac{1}{2}$；
• 如果奖⾦在第 $2$ 扇⻔后⾯，主持⼈只能打开第 $3$ 扇⻔。因此 $𝑃(\overline{𝐴_3}|A_2)=1$；
• 如果奖⾦在第 $3$ 扇⻔后⾯，显然 $𝑃(\overline{𝐴_3}|A_3)=0$。

带入可得 $𝑃(𝐴_1|\overline{𝐴_3})=\dfrac{1}{3}$，因此更换选择后中奖概率更高，$𝑃(𝐴_2|\overline{𝐴_3})=\dfrac{2}{3}$。

更直观的认识：

随机变量

表示将样本点映射到实数域的函数 $𝑋:Ω→𝑅$。

例如，投掷一个骰子，得到的结果有 $1,2,3,4,5,6$。

最简单的实值函数即为结果本身，即投掷结果。

如果考虑投掷两个骰子，那么这个实值函数可以为两者之和和两者中的较⼤值。

例如记随机变量 $𝑋$ 为两个投掷结果之和，则 $𝑋$ 的可能取值为 $2,3,\dots,12$。

记随机变量 $𝑌$ 为两个投掷结果中的较⼤值，则 $𝑋$ 的可能取值为 $1,2,3,4,5,6$。

期望

定义

随机变量在概率意义下的平均值 $E[𝑋]=\sum\limits_{𝜔∈Ω}𝑋(𝜔)𝑃(𝜔)$。

举个例子，假设抽奖得到一⼆三等奖和谢谢惠顾的事件分别为 $A_1,\dots,𝐴_4$，其概率分别为 $0.01,0.02,0.07,0.9$。那么设随机变量 $𝑋$ 代表抽奖得到的奖⾦，$𝑋(𝐴_1)=1000,𝑋(𝐴_2)=500,𝑋(𝐴_3)= 100,𝑋(𝐴_4)=0$，其期望为 $𝐸[𝑋]=1000\times0.01+500\times0.02+100\times0.07+0\times0.9=27$。

这意味着抽奖券⾄少得卖 $27$ 元。

期望的性质

线性：对于任意随机变量 $𝑋$ 和 $𝑌$，满⾜ $E[𝛼𝑋 +𝛽𝑌]=𝛼𝐸[𝑋]+𝛽𝐸[𝑌]$。

期望的线性性是始终成立的，⽆论两随机变量是否独立。

做题最常⽤的性质。

OI 中解概率题的常见套路

• 题目是一个很直接的数学题，直接使⽤数学方法；
• 递推，动态规划（状态之间满⾜拓扑序）；
• 高斯消元（状态之间不满⾜拓扑序）。

矩形粉刷

有一块 $𝑁\times𝑀$ 的矩形⽹格要进⾏粉刷。每次粉刷会等概率选取两个格子，粉刷以这两个格子为顶点的矩形区域。求经过 $K$ 次粉刷后，⾄少被刷了一次的格子数的期望。

$𝑁,𝑀\le1000，𝐾\le100$。

容斥原理

见 oiwiki。