-
个人简介
(原创)超级STL
还没调好
#include<iostream> #include<algorithm> using namespace std; const int N = 1e5+5; struct vec{//约等于标准库中的vector int value[N],n; void push_back(int x) {value[++n] = x;} void pop_back() { value[n] = 0; --n; } void input() { cin>>n; for(int i =1;i<=n;i++) cin>>value[i]; } void output() { for(int i =1;i<=n;i++) cout<<value[i]<<" "; } void erase(int l,int r) { for(int i =l;i<=n-(r-l+1);i++) value[i] = value[i+(r-l+1)]; n -= r-l+1; } void srt(){ sort(value+1,value+n+1); } }; vec operator+(vec a,vec b) { vec c; for(int i =1;i<=a.n;i++)c.push_back(a.value[i]); for(int i =1;i<=b.n;i++)c.push_back(b.value[i]); return c; } bool operator<(vec a,vec b) { for(int i =1;i<=a.n;i++){ if(a.value[i]<b.value[i]) return 1; if(a.value[i]>b.value[i]) return 0; } return 0; } struct str{//约等于标准库中的string char a[N]; int len; str substr(int st,int lth){ str res; for(int i =st;i<st+lth;i++){ res.a[res.len++] = a[i]; } res.len--; return res; } void erase(int l,int r) { for(int i =l;i<=len-(r-l+1);i++) a[i] = a[i+(r-l+1)]; len -= r-l+1; } void input(){//输入 char tmp; while(cin>>tmp){ a[len++] = tmp; } --len; } void output(){//输出 for(int i =0;i<len;i++)cout<<a[i]; } }; bool operator<(str x,str y) { for(int i =0;i<min(x.len,y.len);i++){ if(x.a[i]<y.a[i]) return 1; if(x.a[i]>y.a[i]) return 0; } if(x.len<y.len)return 1; return 0; } str operator+(str x,str y) { str res; for(int i =0;i<x.len;i++){ res.a[res.len++] = x.a[i]; } for(int i =0;i<y.len;i++){ res.a[res.len++] = y.a[i]; } --res.len; return res; } int main(){ }代码
倍增 (st表)
倍增算法详解 倍增算法是一种高效的算法设计技巧,主要用于解决需要快速定位或计算的问题,特别是在处理区间查询、最近公共祖先(LCA)、后缀数组等问题时非常有用。
基本思想 倍增算法的核心思想是通过预处理数据,构建一个"跳跃表"或"倍增表",使得每次查询时可以以2的幂次方的步长快速跳跃,从而将线性时间复杂度优化为对数时间复杂度。
主要应用
- 最近公共祖先(LCA) 预处理:
构建每个节点的2^k级祖先表 时间复杂度:O(n log n) 查询:
先将两个节点调整到同一深度 然后一起向上跳跃寻找LCA 时间复杂度:O(log n) 2. 区间最值查询(RMQ) 使用ST表(Sparse Table)实现:
预处理构建区间长度为2^k的最值表 查询时通过两个重叠的区间组合得到答案 3. 快速幂计算 计算a^b时:
通过分解b的二进制表示 将问题转化为多个a^(2^k)的乘积
#include<bits/stdc++.h> using namespace std; int st[100005][23],lg[100005]; int ask(int l,int r){ int k = lg[r-l+1]; return max(st[l][k],st[r-(1<<k)+1][k]); } signed main(){ int n,m;cin>>n>>m; lg[0] = -1; for(int i =1;i<=n;i++){ lg[i] = lg[i>>1]+1; cin>>st[i][0]; } for(int j=1;(1<<j)<=n;j++){ for(int i =1;i+(1<<j)-1<=n;i++){ st[i][j] = max(st[i][j-1],st[i+(1<<j-1)][j-1]); } } while(m--){ int l,r;cin>>l>>r; cout<<ask(l,r)<<"\n"; } }链表
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点(链表中每一个元素称为结点)组成,结点可以在运行时动态生成。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构,操作复杂。由于不必须按顺序存储,链表在插入的时候可以达到O(1)的复杂度,比另一种线性表顺序表快得多,但是查找一个节点或者访问特定编号的节点则需要O(n)的时间,而线性表和顺序表相应的时间复杂度分别是O(logn)和O(1)。 使用链表结构可以克服数组链表需要预先知道数据大小的缺点,链表结构可以充分利用计算机内存空间,实现灵活的内存动态管理。但是链表失去了数组随机读取的优点,同时链表由于增加了结点的指针域,空间开销比较大。链表最明显的好处就是,常规数组排列关联项目的方式可能不同于这些数据项目在记忆体或磁盘上顺序,数据的存取往往要在不同的排列顺序中转换。链表允许插入和移除表上任意位置上的节点,但是不允许随机存取。链表有很多种不同的类型:单向链表,双向链表以及循环链表。链表可以在多种编程语言中实现。像Lisp和Scheme这样的语言的内建数据类型中就包含了链表的存取和操作。程序语言或面向对象语言,如C,C++和Java依靠易变工具来生成链表。
#include<bits/stdc++.h> using namespace std; struct node{ int data; node * next; }; node * p, *head=NULL,*q; void print(){ p=head; while(p!=NULL){ cout<<p->data<<" "; p=p->next; } cout<<"\n"; } int k,x,y; void del(){ cin>>y; if(y==1){ p=head; head=p->next; delete p; } else{ q=head; for(int i =1;i<y-1;i++){ q=q->next; } p=q->next; q->next=p->next; delete p; } print(); } void insert(){ cin>>k>>x; q=head; p=new node; p->data=x; if(k==1){ p->next=head; head=p; } else{ for(int i =1;i<k-1;i++){ q=q->next; } p->next=q->next; q->next=p; } print(); } int main(){ int n;cin>>n; for(int i =1;i<=n;i++){ int w;cin>>w; p=new node; p->data=w; p->next=head; head=p; } insert(); del(); }神秘网址
https://cdn.luogu.com.cn/upload/image_hosting/z4yt0840.png二分查找
对于区间[a,b]上连续不断且f(a)·f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫二分法。
#include<bits/stdc++.h> using namespace std; int n,a[100005],x,q; int main(){ cin>>n; for(int i =1;i<=n;i++){ cin>>a[i]; } sort(a+1,a+n+1); cin>>q; while(q--){ cin>>x; int l = 1,r = n; while(l<=r){ int mid = (l+r)>>1; if(a[mid]>=x) r = mid-1; else l = mid+1; } if(a[r+1]==x) cout<<r+1<<"\n"; else cout<<"-1\n"; } }Dijkstra
迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的,因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始,采用贪心算法的策略,每次遍历到始点距离最近且未访问过的顶点的邻接节点,直到扩展到终点为止。 [1]一篇发表于2024年的论文证明了迪克斯特拉算法具有普遍最优性。
#include<bits/stdc++.h> #define pii pair<int,int> using namespace std; vector<pii>g[10005]; int dis[10005]; void dijkstra(){ memset(dis,127,sizeof(dis)); priority_queue<pii,vector<pii>,greater<pii>> p; dis[1] = 0; p.push({1,0}); while(p.size()){ int u = p.top().first,disn = p.top().second; p.pop(); if(disn>dis[u]) continue; for(auto i:g[u]){ int v = i.first,w = i.second; if(dis[v]>dis[u]+w){ dis[v] = dis[u]+w; p.push({v,dis[v]}); } } } cout<<dis[n]; } signed main(){ int n,m;cin>>n>>m; for(int i =1;i<=m;i++){ int u,v,w;cin>>u>>v>>w; g[u].push_back({v,w}); } dijkstra(); }SPFA(它死了)
SPFA 算法是 Bellman-Ford算法 的队列优化算法的别称,通常用于求含负权边的单源最短路径,以及判负权环。SPFA 最坏情况下时间复杂度和朴素 Bellman-Ford 相同,为 O(VE)。
#include<iostream> #include<cstring> #include<vector> #include<queue> #define pii pair<int,int> using namespace std; int dis[100005],inq[100005]; vector<pii>g[100005]; int n,m; void spfa(){ memset(dis,127,sizeof(dis)); queue<int>q; q.push(1); dis[1] = 0; inq[1] = 1; while(q.size()){ int u = q.front(); q.pop(); inq[u] = 0; for(auto i:g[u]){ int v = i.first,w = i.second; if(dis[v]>dis[u]+w){ dis[v] = dis[u]+w; if(!inq[v]){ q.push(v); inq[v] = 1; } } } } cout<<dis[n]; } signed main(){ cin>>n>>m; for(int i =1;i<=m;i++){ int u,v,w; g[u].push_back({v,w}); } spfa(); }神秘的东西
这是MAK的抽象画:
⣿⣿⣿⠟⠛⠛⠻⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡟⢋⣩⣉⢻⣿⣿ ⣿⣿⣿⠀⣿⣶⣕⣈⠹⠿⠿⠿⠿⠟⠛⣛⢋⣰⠣⣿⣿⠀⣿⣿ ⣿⣿⣿⡀⣿⣿⣿⣧⢻⣿⣶⣷⣿⣿⣿⣿⣿⣿⠿⠶⡝⠀⣿⣿ ⣿⣿⣿⣷⠘⣿⣿⣿⢏⣿⣿⣋⣀⣈⣻⣿⣿⣷⣤⣤⣿⡐⢿⣿ ⣿⣿⣿⣿⣆⢩⣝⣫⣾⣿⣿⣿⣿⡟⠿⠿⠦⠀⠸⠿⣻⣿⡄⢻ ⣿⣿⣿⣿⣿⡄⢻⣿⣿⣿⣿⣿⣿⣿⣿⣶⣶⣾⣿⣿⣿⣿⠇⣼ ⣿⣿⣿⣿⣿⣿⡄⢿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡟⣰⣿ ⣿⣿⣿⣿⣿⣿⠇⣼⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⢀⣿⣿ ⣿⣿⣿⣿⣿⠏⢰⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⢸⣿⣿ ⣿⣿⣿⣿⠟⣰⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⠀⣿⣿ ⣿⣿⣿⠋⣴⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡄⣿⣿ ⣿⣿⠋⣼⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⣿⡇⢸⣿千万别打开
讲个笑话:
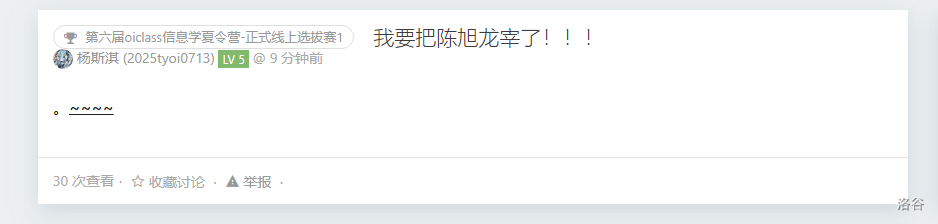
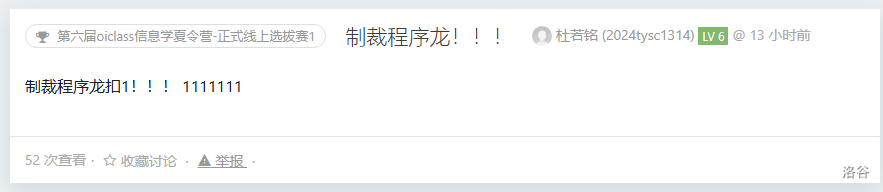
那很抽象了:

What?
Start:2025.9.17 你是第
位访客
$$5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5_{5}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$$Oops!
You are not assigned to this contest.
- 是这样的
Update
- Update 2025.9.17蒟蒻の主页只有4.5k+
- Update 2025.9.19蒟蒻の主页5.1k+字了!!
- Update 2025.9.20蒟蒻の主页6.4k+字了!!!
- Update 2025.9.20蒟蒻の主页8.1k+字了!!!
-
最近活动
- 2025OiClass入门组周赛计划#07 OI
- 2025OiClass入门组周赛计划#05 OI
- 20251204铁外信息学BC班巩固练习 作业
- 2025OiClass入门组周赛计划#04 OI
- 铁外信息学C班训练集20250910 作业
- 2025 CSP-J1初赛模拟测试8 OI
- 2025 CSP-J1初赛模拟测试6 OI
- 2025 CSP-J1初赛模拟测试3 OI
- 铁外信息学B班训练集20250916 作业
- 第六届oiclass信息学夏令营---巩固练习1 IOI(严格)
- 第六届oiclass信息学夏令营-正式线上选拔赛1 IOI(严格)
- 2025TYOI暑期集训结营娱乐赛 XCPC
- 第六届oiclass信息学夏令营Class15-函数 作业
- 第六届oiclass信息学夏令营-模拟测试1(订题) 作业
- 第六届oiclass信息学夏令营Class9-一维数组的定义和基础应用 作业
- 第六届oiclass信息学夏令营Class7-循环结构-while语句 作业
- 第六届oiclass信息学夏令营Class5-循环结构-for语句基础 作业
- 第六届oiclass信息学夏令营Class3作业-if语句 作业
- 第六届oiclass信息学夏令营Class1作业-程序结构 作业
- 2025铁一集团新苗day1作业-C++程序结构 作业
- 铁外信息学C班6月份作业 作业
- 铁外信息学C班模拟赛0412 IOI
- 小六春季班——多维DP+差值DP+双指针 作业
- 第四届 TYCPC 程序设计大赛(重现补题赛) IOI
- 小六春季班——倍增算法 作业
- 小六春季班——区间DP2之区间合并 作业
- 小六春季班——区间DP1之区间分割 作业
- 【oiClass公益赛】2025CSP-J模拟赛#17 OI
- 【oiClass公益赛】2025CSP-J模拟赛#16 OI
- 【oiClass公益赛】2025CSP-J模拟赛#15 OI
- 【oiClass公益赛】2025CSP-J模拟赛#14 OI
- 【oiClass公益赛】2025CSP-J模拟赛#13 OI
- 【oiClass公益赛】2025CSP-J模拟赛#12 OI
- 【oiClass公益赛】2025CSP-J模拟赛#11 OI
- 【oiClass公益赛】2025CSP-J模拟赛#10 OI
- 【oiClass公益赛】2025CSP-J模拟赛#09 OI
- 【oiClass公益赛】2025CSP-J模拟赛#08 OI
- 【oiClass公益赛】2025CSP-J模拟赛#07 OI
- 【oiClass公益赛】2025CSP-J模拟赛#06 OI
- 【oiClass公益赛】2025CSP-J模拟赛#05 OI
- 【oiClass公益赛】2025CSP-J模拟赛#04 OI
- 【oiClass公益赛】2025CSP-J模拟赛#03 OI
- 【oiClass公益赛】2025CSP-J模拟赛#02 OI
- 2024小六冬令营——背包动态规划2 作业
- 2024小六冬令营——背包动态规划1 作业
- 2024小六冬令营——二维动规之最长公共子序列 作业
- 2024小六冬令营——二维线性动态规划规 作业
- 2024小六冬令营——线性动规之最长不下降子序列 作业
- 2024小六冬令营——线性动态规划基础 作业
- 2024小六——二分搜索2 作业
- 2024小六冬令营——二分搜索1 作业
- 2024小六冬令营《广度优先搜索》 作业
- 2024小六冬令营《队列》 作业
- 2024小六秋季班第十四课《深度优先搜索算法2》 作业
- 2024小六秋季班第十三课《深度优先搜索算法1》 作业
- 第三届TYCPC重现赛 XCPC
- 2024小六秋季班第十二课《递归算法2》 作业
- 2024小六秋季班第十一课《递归算法1》 作业
- 2024小六秋季班第九课《栈结构》 作业
- 2024小六秋季班第七课《前缀和&差分前缀和》 作业
- CSP-X2024 山东小学组二轮试题(上半场) 作业
- 2024小六秋季班第七课《贪心算法》 作业
- 2024小六秋季班第六课《枚举算法》 作业
- 2024小六秋季班测试1改题 作业
- 2024小六秋季班第四课《模拟算法》 作业
- 2024小六秋季班第三课《排序和结构体排序》 作业
- 2024小六秋季班第二课《位运算》 作业
- 2024小六秋季班第一课《进制转换》 作业
- 2024oiClass入门组周赛计划#18 IOI
- 2024oiClass入门组周赛计划#17 IOI
- 2024oiClass入门组周赛计划#16 IOI
- 2024oiClass入门组周赛计划#15 IOI
- 2024oiClass入门组周赛计划#14 IOI
- 2024oiClass入门组周赛计划#13 IOI
- 2024oiClass入门组周赛计划#12 IOI
- 2024oiClass入门组周赛计划#11 IOI
- 2024oiClass入门组周赛计划#04 IOI
- 2024oiClass入门组周赛计划#03 IOI
- 2024oiClass入门组周赛计划#02 IOI
- 2024oiClass入门组周赛计划#01 IOI
- 第五届oiClass信息学夏令营线上正式邀请赛3 OI
- 第五届oiClass信息学夏令营线上正式邀请赛2 OI
- 第五届oiClass信息学夏令营线上正式邀请赛1 OI
- 第五届oiClass信息学夏令营线上模拟测试3 OI
-
Stat
-
Rating
